Содержание
Шина 11,5/80-15,3 16 н.с. 141A8 IM-21 NorTec
Главная
>
Шины>Шина 11,5/80-15,3 16 н.с. 141A8 IM-21 NorTec
Увеличить
| ID | 11230010123 |
| Цена | 13 250 руб |
| Типоразмер (мм) | 300/80-15,3 |
| Типоразмер (inch) | 11,5/80-15,3 |
| Типоразмер (dot) | |
| Производитель | АШК |
| Модель | IM-21 |
| Норма слойности | 16 |
| Индексы нагрузки/скорости | 141А8 |
| Артикул | ъ1000015350 |
| Тип (TT,TL) | Бескамерная |
| Комплектность | Покрышка |
| Бренд | NorTec |
| Серия | |
| Посадочный диаметр | 15.3 |
| Ширина профиля (мм) | 300 |
| Ширина профиля (дюйм) | 11.5 |
| Высота профиля | 80 |
| Наружный диаметр (мм) | 845 |
| Фактическая ширина профиля (мм) | 290 |
| Статический радиус (мм) | 0 |
| Путь за оборот (мм) | 0 |
| Рекомендуемый диск | 9. 00-15.3 |
| Допустимые диски | |
| Рисунок | |
| Вес шины (кг) | 0 |
| Конструкция | Диагональная |
| Применение | с/х |
| Норма загрузки фуры 82 м. куб. | 429 |
| Норма загрузки контейнера 40 фут. | 430 |
Описание
шины
Усиленная 11.5/80-15.3
Больше информации о продукте
Если вы хотите купить усиленную, но недорогую шину 11.5/80-15.3, то Нортек IM-21 — это то, что надо. 16-ти слойная, бескамерная, с очень хорошим индексом нагрузки даже на скорости 40 км/ч.
Покупатели этого товара так же приобрели:
Похожие товары:
Шина 11,5/80-15,3 130A8 IM…
Шина 12,5/80-15,3 152A2…
Шина 10,0/75-15,3 122A8 /.
..Шина 11,5/80-15,3 139A8…
Шина 11,5/80-15,3 131А8 /…
Шина 12,5-15,3 142A8 / 138B…
Шина 10,0/75-15,3 123А6 /…
Шина 10,0/75-15,3 127A6…
Шина 11,5/80-15,3 139А8 14…
Шина 11,5/80-15,3 139A8 16…
Шина 12,5/80-15,3 141A8 14.
..Шина 12,5/80-15,3 142A6 /…
Шина 10,0/75-15,3 111A6 /…
Шина 11,5/80-15,3 123A6 /…
Шина 11,5/80-15,3 130A8 10…
Шина 11,5/80-15,3 10 н.с….
Шина 11,5/80-15,3…
Шина 11,5/80-15,3 135A8 12…
Шина 10,0/75-15,3 10 н.
с….Шина 10,0/75-15,3 6 н.с….
Шина 10,0/75-15,3 10 н.с….
Шина 10,0/75-15,3 12 н.с….
Шина 12,5/80-15,3 144А8 16…
Шина 11,5/80-15,3 14 н.с….
Шина 10,0/75-15,3 10 н.с….
Шина 11,5/80-15,3 10 н.с….
Шина 10,0/75-15,3 6 н.
с….Шина 10,0/75-15,3 10 н.с….
..
..
с….
с….Каталог
ЛК РФ Статья 21. Строительство, реконструкция, капитальный ремонт, ввод в эксплуатацию и вывод из эксплуатации, снос, ликвидация и консервация объектов капитального строительства, не связанных с созданием лесной инфраструктуры \ КонсультантПлюс
Подготовлена редакция документа с изменениями, не вступившими в силу
ЛК РФ Статья 21. Строительство, реконструкция, капитальный ремонт, ввод в эксплуатацию и вывод из эксплуатации, снос, ликвидация и консервация объектов капитального строительства, не связанных с созданием лесной инфраструктуры
(в ред. Федерального закона от 02.07.2021 N 301-ФЗ)
(см. текст в предыдущей редакции)
1. Строительство, реконструкция, капитальный ремонт, ввод в эксплуатацию и вывод из эксплуатации объектов капитального строительства, не связанных с созданием лесной инфраструктуры, на землях лесного фонда допускаются при использовании лесов в целях:
1) осуществления геологического изучения недр, разведки и добычи полезных ископаемых;
2) строительства и эксплуатации водохранилищ и иных искусственных водных объектов, создания и расширения территорий морских и речных портов, строительства, реконструкции и эксплуатации гидротехнических сооружений;
3) строительства, реконструкции и эксплуатации линейных объектов;
4) создания и эксплуатации объектов лесоперерабатывающей инфраструктуры;
5) осуществления рекреационной деятельности;
6) осуществления религиозной деятельности.
2. Строительство, реконструкция, капитальный ремонт, ввод в эксплуатацию и вывод из эксплуатации объектов капитального строительства, не связанных с созданием лесной инфраструктуры, на землях иных категорий, на которых расположены леса, допускаются в случаях, определенных другими федеральными законами в соответствии с целевым назначением этих земель.
3. При строительстве, реконструкции, капитальном ремонте, вводе в эксплуатацию и выводе из эксплуатации объектов капитального строительства, не связанных с созданием лесной инфраструктуры, используются в первую очередь земли, не занятые лесными насаждениями, а также земли, занятые лесными насаждениями, указанными в части 3 статьи 29 настоящего Кодекса, если иное не установлено настоящим Кодексом.
4. Сплошные рубки лесных насаждений для строительства, реконструкции, капитального ремонта объектов капитального строительства в целях, предусмотренных пунктами 4 — 6 части 1 настоящей статьи, не допускаются.
5. В целях, предусмотренных пунктами 1 — 3 части 1 настоящей статьи (в том числе в целях проведения аварийно-спасательных работ), допускаются выборочные рубки и сплошные рубки деревьев, кустарников, лиан, в том числе в охранных зонах и санитарно-защитных зонах, предназначенных для обеспечения безопасности граждан и создания необходимых условий для эксплуатации соответствующих объектов.
6. В защитных лесах предусмотренные частью 5 настоящей статьи выборочные рубки и сплошные рубки деревьев, кустарников, лиан допускаются в случаях, если строительство, реконструкция, капитальный ремонт и эксплуатация объектов капитального строительства, не связанных с созданием лесной инфраструктуры, в целях, предусмотренных пунктами 1 — 3 части 1 настоящей статьи, не запрещены или не ограничены в соответствии с законодательством Российской Федерации.
7. Объекты капитального строительства, связанные с организацией указанной в пункте 1 части 1 настоящей статьи деятельности, по истечении сроков выполнения соответствующих работ подлежат сносу, консервации или ликвидации в соответствии с законодательством о недрах.
8. Объекты капитального строительства, не связанные с созданием лесной инфраструктуры и являющиеся гидротехническими сооружениями, по окончании срока их эксплуатации подлежат сносу, консервации или ликвидации в соответствии с водным законодательством и законодательством о безопасности гидротехнических сооружений.
9. Земли, которые использовались для строительства, реконструкции, капитального ремонта или эксплуатации объектов капитального строительства, не связанных с созданием лесной инфраструктуры, подлежат рекультивации.
10. Перечень объектов капитального строительства, не связанных с созданием лесной инфраструктуры, утверждается Правительством Российской Федерации для защитных лесов, эксплуатационных лесов, резервных лесов.
КонсультантПлюс: примечание.
Ч. 11 ст. 21 не применяется при использовании лесов в целях осуществления религиозной деятельности (ФЗ от 04.12.2006 N 201-ФЗ).
11. При использовании лесов не допускаются строительство и эксплуатация объектов капитального строительства, отнесенных в соответствии с федеральными законами к жилым домам.
12. Предельные (максимальные и (или) минимальные) параметры разрешенного строительства, реконструкции указанных в части 1 настоящей статьи объектов капитального строительства и определенные с учетом видов использования лесов требования к таким объектам, за исключением линейных объектов, утверждаются Правительством Российской Федерации.
Решение неравенств с помощью пошагового решения математических задач
В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача
«Найдите число, которое при прибавлении к 3 дает 7»
можно записать так:
3 + ? = 7, 3 + n = 7, 3 + x = 1
и т. д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.
Уравнение:
3 + x = 7
будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1. Определить, является ли значение 3 решением уравнения член.
4(3) — 2 = 3(3) + 1
12 — 2 = 9 + 1
10 = 10
Ответ. 3 это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.
Пример 2 Найдите решение каждого уравнения путем проверки.
а. х + 5 = 12
б. 4 · x = -20
Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.
1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.
Если к обоим элементам добавляется или вычитается одно и то же количество
уравнения, полученное уравнение эквивалентно исходному
уравнение.
В символах
a — b, a + c = b + c и a — c = b — c
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
x + 3 = 7
путем вычитания 3 из каждого члена.
Решение Вычитание 3 из каждого члена дает
x + 3 — 3 = 7 — 3
или
x = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же. для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.
Объединение одинаковых членов дает
x — 2 = 10
Добавление 2 к каждому члену дает
x-2+2 =10+2
x = 12
Чтобы решить уравнение, мы используем сложение-sub тяга свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим
2x + 1- 1 = x — 2- 1
2x = x — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2x-x = x — 3 — х
х = -3
где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнение
2(-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не заботясь о смене знака.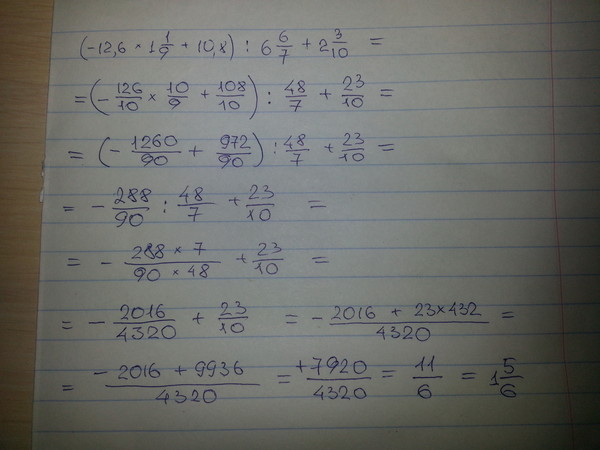
Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько различные способы применения вышеуказанного свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала прибавим -3x к каждому элементу, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
где переменная имеет отрицательный коэффициент. Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2х-2х + 9 = 3х- 9-2х+ 9
9 = х
откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
Решенные уравнения с использованием Свойства Отдела
Рассмотрим уравнение
3x = 12
Решение этого уравнения равно 4.
Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получаем уравнения
, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения разделить на одно и то же (отличное от нуля)
полученное уравнение эквивалентно исходному уравнению.
В символах
эквивалентны уравнениям.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Деление обоих членов на -4 дает
При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые члены, чтобы получить
5y = 20
Затем, разделив каждый член на 5, мы получаем
В следующем примере мы используем дополнение — свойство вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее , объединение одинаковых членов дает
3x = -9
Наконец, мы делим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ, ИСПОЛЬЗУЯ СВОЙСТВО УМНОЖЕНИЯ решение этого уравнения равно 12. Также обратите внимание, что если умножая каждый член уравнения на 4, мы получаем уравнения
, решение которых также равно 12. В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
В символах
a = b и a·c = b·c (c ≠ 0)
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
, умножив каждый член на 6.
Решение Умножив каждый член на 6, получим
дроби.
Пример 2 Решить
Решение Сначала умножьте каждый член на 5, чтобы получить
Теперь разделите каждый член на 3,
Пример 3 Решите .
Решение Сначала упростим над дробной чертой, чтобы получить
Затем умножим каждый член на 3, чтобы получить
Наконец, разделив каждый член на 5, получим
ДОПОЛНИТЕЛЬНОЕ СОЛНЦЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени. Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.
Шаги для решения уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестного в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство Division, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем +2x и +7 к каждому члену и объединяем одинаковые члены, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы делим каждый член на 7, чтобы получить
В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Сначала мы объединяем одинаковые члены, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы делим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами.
Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.
Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть
d = rt
(24) = (3)t
8 = t
Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие. Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить
, откуда по симметричному закону
В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить
затем разделив каждый член на a, мы получим
Упростить: 12/5=21/x Алгебра-решатель тигра от обе части уравнения:
12/5-(21/x)=0
Пошаговое решение:
Шаг 1 :
21
Упростить ——
Икс
Уравнение в конце шага 1 :
12 21 —— — —— = 0 5 х
Шаг 2 :
12
Упростить ——
5
Уравнение в конце шага 2 :
12 21 —— — —— = 0 5 х
Шаг 3 :
Вычисление наименьшего общего кратного:
3.1 Найдите наименьшее общее кратное
Левый знаменатель: правый знаменатель: x
| Простое число Фактор | Левый Знаменатель | Правый Дено minator | L. C.M = Max {Left,Right} |
|---|---|---|---|
| 5 | 1 | 0 | 1 |
| Произведение всех Прайм Факторс | 5 | 1 | 5 |
| Алгебраический Множитель | Левый Знаменатель | L.C.M = Макс. {Левое, Право} |
|---|---|---|
| x | 0 | 1 |
Наименьшее общее кратное:
5x
Вычисление множителей:
3.2 Вычисление множителей для двух дробей
Обозначьте наименьшее общее кратное через L.C.M
Обозначьте левый множитель через Left_M
Обозначьте правый множитель через Right_M
Обозначьте левый знаменатель через L_Deno
Обозначьте правый множитель плоскогубцы R_Deno
Left_M = L.
C.M / L_Deno = x
Right_M = L.C.M / R_Deno = 5
Создание эквивалентных дробей :
3.3 Преобразуйте две дроби в эквивалентные дроби
Две дроби называются эквивалентными, если они имеют одинаковое числовое значение.
Например: 1/2 и 2/4 эквивалентны, y/(y+1) 2 и (y 2 +y)/(y+1) 3 также эквивалентны.
Чтобы рассчитать эквивалентную дробь, умножьте числитель каждой дроби на соответствующий множитель.
Л. Мульти. • L. Num. 12 • х
"="
LCM 5x
Р. Мульт. • R.Число. 21 • 5
"="
LCM 5x
Сложение дробей, имеющих общий знаменатель:
3.4 Сложение двух эквивалентных дробей
Сложение двух эквивалентных дробей, которые теперь имеют общий знаменатель
Сложение числителей вместе, подведение суммы или разности к общему знаменателю, затем уменьшение до наименьшего термины если возможно:
12 • x - (21 • 5) 12x - 105
"="
5х 5х
Шаг 4 :
Вытягивание одинаковых членов:
4.