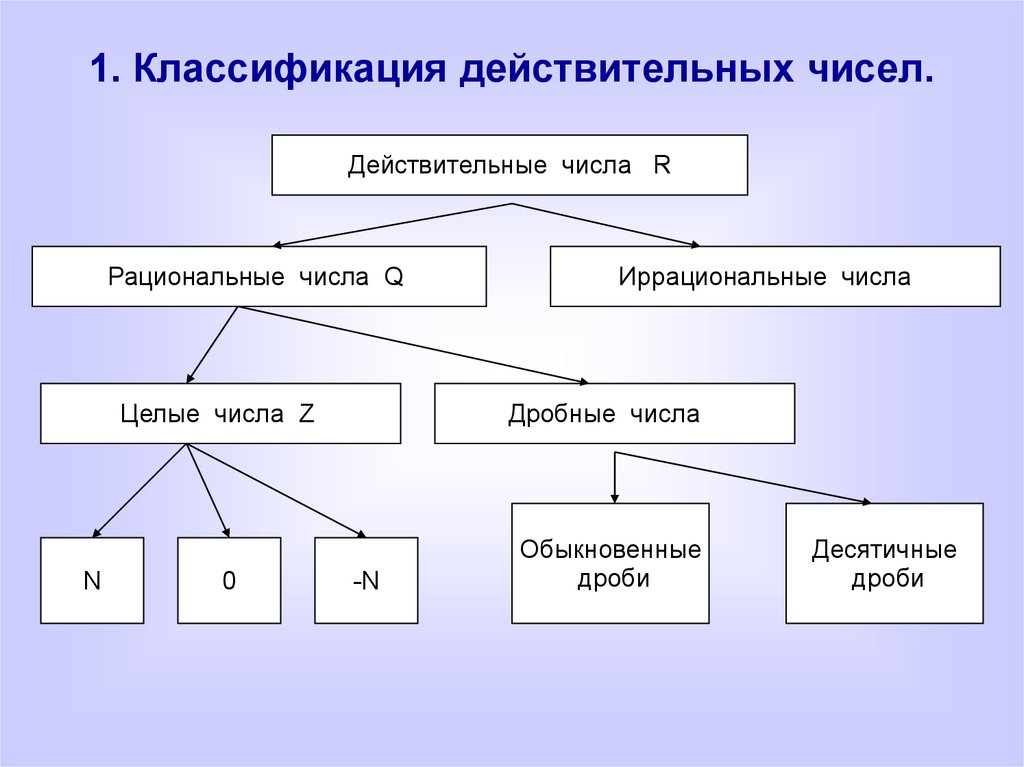
Содержание
Что такое действительное число? Ответ на webmath.ru
Содержание:
- Определение действительного числа
- Сложение действительных чисел
- Вычитание действительных чисел
- Умножение действительных чисел
- Деление действительных чисел
- Свойства операции сложения действительных чисел
- Свойства операции умножения действительных чисел
Определение действительного числа
Определение
Действительными или вещественными числами
называются все положительные числа, отрицательные числа и нуль.
Множество действительных чисел объединяет в себе множество
рациональных и
иррациональных чисел. Обозначается множество действительных чисел $R$ .
Например. $\frac{2}{3} ; 0,754 ;-23 ;-\frac{5}{4} ; 113 ;-\sqrt[3]{2} ;-2,34 ; \frac{1}{\pi}$
— все это действительные числа.
На множестве действительных чисел можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление.
Сложение действительных чисел
Для любых двух действительных чисел $a$ и $b$ существует единственное число $c$, называемое суммой этих чисел. При этом
Свойства операции сложения действительных чисел
Коммутативный закон сложения: для любой пары чисел $a$ и $b$
$$a+b=b+a$$
Ассоциативный закон сложения: для любой тройки чисел $a$, $b$ и $c$
$$(a+b)+c=a+(b+c)$$
Нейтральный элемент: существует число, обозначаемое 0 и называемое нулем, такое, что для любого числа $a$
$$a+0=0+a=a$$
Для любого числа $a$ существует число, обозначаемое $(-a)$, такое, что
$$a+(-a)=(-a)+a=0$$
число $(-a)$ называется противоположным числу $a$ ;
Вычитание действительных чисел
Для любых двух действительных чисел $a$ и $b$ число $c=a+(-b)$ называется разностью чисел $a$ и $b$, и обозначается
Пример
Задание. Найти сумму и разность действительных чисел $23$ и $12,4$
Найти сумму и разность действительных чисел $23$ и $12,4$
Решение. Сумма заданных чисел равна $23+12,4=35,4$
Разность: $23-12,4=10,6$
Ответ.
$23+12,4=35,4$
$23-12,4=10,6$
Умножение действительных чисел
На множестве действительных чисел определена операция называемая умножением. Для любых двух действительных чисел
$a$ и $b$ существует единственное число $c$, называемое их произведением и обозначаемая
Свойства операции умножения действительных чисел
Коммутативный закон сложения: для любой пары чисел $a$ и $b$
$$a \cdot b=b \cdot a$$
Ассоциативный закон умножения: для любой тройки чисел $a$, $b$ и $c$
$$(a \cdot b) \cdot c=a \cdot(b \cdot c)$$
Нейтральный элемент: существует число, обозначаемое символом 1 и называемое единицей, такое, что для любого числа $a$
$$a \cdot 1=1 \cdot a$$
Для любого числа $a$, отличного от нуля, существует число, обозначаемое $$(1 / a)$$, такое, что
$$a \cdot \frac{1}{a}=\frac{1}{a} \cdot a=1$$
число $$(1 / a)$$ называется обратным числу $a$ ;
Деление действительных чисел
Для любых двух действительных чисел $a$ и $b$ ( $b$ отлично от нуля) существует число $c$
$$c=a \cdot \frac{1}{b}$$
называется частным от деления числа $a$ на $b$, и обозначается
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение и частное действительных чисел $1,2$ и $5$
Найти произведение и частное действительных чисел $1,2$ и $5$
Решение. Произведение заданных чисел равно $1,2 \cdot 5=6$
Частное: $1,2 : 5=1,2 \cdot \frac{1}{5}=1,2 \cdot 0,2=0,24$
Ответ.
$1,2 \cdot 5=6$
$1,2 : 5=0,24$
Операции сложения и умножения действительных чисел связаны законом дистрибутивности умножения относительно сложения:
$$(a+b) \cdot c=a \cdot c+b \cdot c$$
Читать дальше: что такое четное число.
определение, примеры, представления, координатная прямая
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Определение 1
Действительные числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается через R.
Множество действительных чисел обозначается через R.
Данное определение можно записать иначе с учетом следующего:
- Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
- Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.
Определение 2
Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0,578; -38; 265; 0,145(3); log512.
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
- Натуральные числа.
- Целые числа.
- Десятичные дроби.
- Обыкновенные дроби.
- Смешанные числа.
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Например, значения выражений sin23π·e-285·10log32 и tg676693-8π32 — действительные числа.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор:
Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Вычитание целых чисел
Следующая статья
Рациональные числа
- Арифметические операции над действительными числами
- Взаимно обратные числа
- Вычитание десятичных дробей
- Вычитание натуральных чисел
- Вычитание натуральных чисел
- Все темы по математике
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
Контрольная работа
Вид работы:
Контрольная работа
Выполнена:
27 октября 2022 г.

Стоимость:
3 800 руб
Заказать такую же работу
Выполнить заданий
Вид работы:
Домашняя работа
Выполнена:
23 сентября 2022 г.

Стоимость:
1 100 руб
Заказать такую же работу
Контрольная работа задание к разделу вариант задание к разделу вариант Контрольная работа задание к разделу задание к разделу задание к разделу задание к разделу везде вариант только
Вид работы:
Контрольная работа
Выполнена:
17 сентября 2022 г.

Стоимость:
1 700 руб
Заказать такую же работу
Расчеты фундаментов
Вид работы:
Практическая работа
Выполнена:
7 августа 2022 г.

Стоимость:
2 900 руб
Заказать такую же работу
выполнить задание
Вид работы:
Контрольная работа
Выполнена:
21 июля 2022 г.

Стоимость:
1 300 руб
Заказать такую же работу
ДопГлавыМатематики
Заказать такую же работу
Смотреть все работы по нефтегазовому машиностроению
Real Numbers — GeeksforGeeks
В математике вещественное число — это значение непрерывной величины, которое может представлять расстояние вдоль линии. Действительные числа включают в себя как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2, 7/8, 2,5) и иррациональные числа, такие как √7, π и т. д., являются действительными числами.
Действительные числа включают в себя как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2, 7/8, 2,5) и иррациональные числа, такие как √7, π и т. д., являются действительными числами.
Никогда не думал, что мы можем считать вещи, но как мы можем считать. Мы можем считать, используя числа. Но числа также бывают разных типов: некоторые имеют отрицательные значения, некоторые имеют положительные значения, некоторые очень большие, некоторые очень маленькие, некоторые в математических операциях, поэтому существует много типов чисел.
Число или система счисления — это система представления чисел. В математике существуют различные типы систем счисления, такие как двоичная, десятичная и т. д. Система счисления представляет собой то, как число должно быть записано.
Числа разделены на следующие типы:
- Натуральные номера
- Целые номера
- Целые числа
- Рациональные номера
- Иррациональные номера
Натуральные номера
Натуральные номера — это те, которые используются вами в вашем повседневную жизнь считать как 1, 2, 3 …. . Это положительные числа, потому что мы не можем считать в отрицательном выражении.
. Это положительные числа, потому что мы не можем считать в отрицательном выражении.
Предположим, вы выбираете число из 1, 2, 3, 4, 5…… и так до бесконечности. Эти числа известны как натуральные числа. Эти натуральные числа обозначаются символом N.
Целые числа
Целые числа — это числа, в которых к натуральным числам добавляется одно число. Добавление 0 к натуральным числам превращает серию в набор целых чисел.
0, 1, 2, 3, 4, 5……и так до бесконечности. Эти числа известны как целые числа. Эти целые числа обозначаются символом W.
Целые числа
Все числа, которые имеют полное значение, известны как целые числа, и существует два типа целых чисел: первое — отрицательное, а второе — положительное.
….-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5……и так до бесконечности. Эти числа известны как целые числа и обозначаются символом Z.
Рациональные числа
В математике рациональное число — это число, которое может быть выражено как дробь p/q двух целых чисел, числитель p и не -нулевой знаменатель q, такой как 2/7.
Пример: 25 можно записать как 25/1, так что это рациональное число.
Иррациональные числа
Иррациональные числа — это числа, которые не могут быть выражены в виде p/q, где p и q — целые числа, а q ≠ 0. Короче говоря, иррациональные числа — это действительные числа, которые не являются рациональными числами.
Пример: √3, √5, π и т. д. Эти числа известны как иррациональные числа.
Вопрос 1. Найдите три рациональных числа между 6 и 7.
Ответ.
Три рациональных числа от 6 до 7: 13/2, 20/3 27/4.
Вопрос 2. Можете ли вы определить следующие серии 0, 1, 2, 3, 4, 5, 6, 7 ……?
Ответ.
Это группа чисел, представляющая целые числа.
Таблица реальных чисел
Представление чисел на прямой Число
Числовая линия представляет собой представление чисел с фиксированным интервалом между ними на прямой линии. Числовая строка содержит все типы чисел, такие как натуральные числа, рациональные числа, целые числа и т. д.
Числовая строка содержит все типы чисел, такие как натуральные числа, рациональные числа, целые числа и т. д.
Как показано в приведенной выше числовой строке, 0 присутствует в середине строки. Положительные целые числа записываются справа от нуля, тогда как отрицательные целые числа записываются слева от нуля.
Рациональные числа записываются между числами, на которых они лежат. Например, 3/2 равно 1,5, поэтому оно отмечено между 1 и 2. Это показывает, что число 3/2 лежит где-то между 1 и 2.
Точно так же число 13/4 лежит между 3 и 4. Итак, мы отметили это между 3 и 4. Число -50/9лежит между -5 и -6. Итак, мы отметили его между -5 и -6 на числовой прямой.
Вопрос: Представьте следующие числа на числовой прямой.
(I) 23/5
(II) 6
(III) -33/7
9003
Десятское расширение номера реального номера
Экспрессии. его представление по основанию равно 10 (т. е. в десятичной системе). В этой системе каждый «десятичный знак» состоит из цифры от 0 до 9.. Эти цифры расположены так, что каждая цифра умножается на степень 10, уменьшаясь слева направо.
его представление по основанию равно 10 (т. е. в десятичной системе). В этой системе каждый «десятичный знак» состоит из цифры от 0 до 9.. Эти цифры расположены так, что каждая цифра умножается на степень 10, уменьшаясь слева направо.
Можем ли мы представить 13/4 в другой форме, которая может показать его точное значение на числовой прямой?
Да. Мы можем записать его в десятичных дробях, что дает его точное значение. Давайте расширим 13/4
Итак, 13/4 также можно записать как 3,25.
Теперь возьмем другой пример. Давайте расширим 1/3
Итак, 1/3 также можно записать как 0,3333…… Мы также можем записать это как
Аналогично, 1/7 можно записать как 0,142857142857142857… или . Это можно определить как повторяющиеся десятичные дроби.
Последовательное увеличение
Процесс представления и визуализации действительных чисел на числовой прямой через увеличительное стекло известен как последовательное увеличение.
Возьмем в качестве примера 3,25
Мы можем сказать, что 3,25 определенно лежит между 3 и 4. Можем ли мы сказать, где именно оно лежит? Да, мы можем сделать это, используя последовательное увеличение.
Можем ли мы сказать, где именно оно лежит? Да, мы можем сделать это, используя последовательное увеличение.
В первой строке мы видим, что 3,25 лежит между 3 и 4. Теперь сделайте шаг вперед. Теперь мы масштабируем между 3,2 и 3,3. Здесь мы обнаружили, что 3,25 находится между 3,2 и 3,3. Таким образом, мы представили 3,25 на числовой прямой, используя последовательное увеличение.
Операции над действительными числами
Мы знаем, что можем выполнять математические операции над рациональными числами. Например, мы можем складывать, делить, умножать и вычитать рациональное число с другим числом. В результате мы также получаем рациональное число.
Точно так же мы можем выполнять математические операции и с иррациональными числами, но результат может быть рациональным или иррациональным.
Примеры примеров
Пример 1. Сложите √3 и √5
Решение:
(√3 + √5)
Теперь ответом является иррациональное число.
Пример 2. Умножьте √3 и √3.
Решение:
√3 × √3 = 3
Теперь ответ — рациональное число.
Таким образом, мы можем сказать, что результат математических операций над иррациональными числами может быть рациональным или иррациональным.
Теперь сложите рациональное число с иррациональным числом.
Пример 3. Сложите 2 и √5
Решение:
(2 + √5)
Теперь ответ — иррациональное число.
Пример 4: Упростите выражение: (2 + √3)(5 + √3)
Решение:
(2 + √3)(5 + √3)
= 10 + 2√3 + 5√3 + 3
= 13 + 7√3
Теперь ответ — иррациональное число.
Понимание реальных и сложных чисел в алгебре
Ключевые члены
o Реальное число
o Комплексное число
o Натуральное число
o Rational Number
O Иррационное число
o CommutAtbity
o Иррационное число
o Commutatbity
O Иррационное число 9000 2
O Иррационное число o Ассоциативность
o Распределение
o Identity
o обратный
Цели
O Изучите, что такое набор реальных чисел
o Признайте некоторые основные подмные реальные числа и почему они применимы и т. д.) обычно являются действительными числами. А действительное число — это любое число, которое можно разместить на числовой прямой, простирающейся до бесконечности как в положительном, так и в отрицательном направлениях. Эта числовая строка проиллюстрирована ниже числом 4,5, отмеченным в качестве примера закрытой точкой. Набор действительных чисел часто обозначается символом .
д.) обычно являются действительными числами. А действительное число — это любое число, которое можно разместить на числовой прямой, простирающейся до бесконечности как в положительном, так и в отрицательном направлениях. Эта числовая строка проиллюстрирована ниже числом 4,5, отмеченным в качестве примера закрытой точкой. Набор действительных чисел часто обозначается символом .
На приведенной выше иллюстрации, конечно, показана только часть числовой строки (было бы невозможно показать ее целиком), и помечены только определенные числа (–1, 0, 1 и т. д.). Таким образом, действительным числом может быть 8, 4,357, -3/5, π, 9.0287 или любой другой подобный номер. Конкретное представление, будь то дробь, десятичная дробь или другое представление, не имеет значения. Возможно, лучший способ описать действительное число — определить числа, которые не являются действительными числами . Бесконечность (∞) — это , а не — действительное число, хотя оно больше любого заданного действительного числа; также не является действительным числом, так как не существует числа, квадрат которого равен –1.
В качестве краткого отступления давайте определим мнимое число 9.0287 (так называемый, потому что не существует эквивалентного «настоящего числа») с использованием буквы i ; затем мы можем создать новый набор чисел, называемый комплексными числами. Комплексное число — это любое число, включающее и . Таким образом, 3 i , 2 + 5,4 i и –π i — комплексные числа. (На самом деле действительные числа являются подмножеством комплексных чисел — любое действительное число х может быть записано как х + 0 i , что является комплексным представлением.) Комплексные числа — важная часть алгебры, и они имеют отношение к таким вещам, как решения полиномиальных уравнений. Символ часто используется для набора комплексных чисел.
Подмножества действительных чисел
Действительные числа включают в себя диапазон явно различных чисел: например, числа без десятичных знаков, числа с конечным числом десятичных разрядов и числа с бесконечным числом знаков. десятичные знаки. Давайте рассмотрим некоторые подмножества действительных чисел, начиная с самых основных.
десятичные знаки. Давайте рассмотрим некоторые подмножества действительных чисел, начиная с самых основных.
Сначала дети изучают «счетные» числа: 1, 2, 3 и т. д. Формально они называются 9.0047 натуральных чисел , а множество натуральных чисел часто обозначают символом . Если мы добавим к этому набору число 0, мы получим целых чисел . Кроме положительных чисел, есть и отрицательные числа: если мы включим в набор отрицательные значения каждого целого числа, то получим так называемые целых чисел . Набор целых чисел часто обозначается символом .
В дополнение к целым числам множество действительных чисел также включает дробные (или десятичные) числа. Между любыми двумя целыми числами существует бесконечное число дробных значений. Рассмотрим, например, 1 и 2; между этими числами находятся значения 1,1, 1,11, 1,111, 1,1111 и т. д. Очевидно, мы могли бы добавить столько дополнительных знаков после запятой, сколько пожелаем. Множество действительных чисел делится на два принципиально разных типа чисел: рациональные числа и иррациональные числа. А рациональное число — это число, которое может быть эквивалентно выражено в виде дроби , где a и b оба являются целыми числами, а b не равно 0. Таким образом, рациональные числа включают целые числа, а также конечные десятичные дроби и повторяющиеся десятичные дроби (например, 0,126126126). Символ часто используется для обозначения набора рациональных чисел. Иррациональное число , с другой стороны, является неповторяющимся десятичным числом без завершения. Множество действительных чисел полностью состоит из рациональных и иррациональных чисел.
Множество действительных чисел делится на два принципиально разных типа чисел: рациональные числа и иррациональные числа. А рациональное число — это число, которое может быть эквивалентно выражено в виде дроби , где a и b оба являются целыми числами, а b не равно 0. Таким образом, рациональные числа включают целые числа, а также конечные десятичные дроби и повторяющиеся десятичные дроби (например, 0,126126126). Символ часто используется для обозначения набора рациональных чисел. Иррациональное число , с другой стороны, является неповторяющимся десятичным числом без завершения. Множество действительных чисел полностью состоит из рациональных и иррациональных чисел.
Хотите узнать больше? Почему бы не пройти онлайн-курс по алгебре?
Давайте рассмотрим эти подмножества действительных чисел:
Натуральные числа, = Целые числа Целые числа, Рациональные числа, Иррациональные числа Комплексные числа, |
Практическая задача: Определите, какие из следующих чисел принадлежат : {0, i , 3,54, , ∞}.
Решение: Если число можно записать как , где a и b — целые числа, то это число рационально (т. е. оно входит в набор ). Обратите внимание на следующее:
Таким образом, каждое из этих чисел рационально. Число и мнимое, поэтому оно не принадлежит реальным числам. Точно так же ∞ не является действительным числом; i и ∞ поэтому не входят в набор .
Свойства действительных чисел
Теперь, когда вы знаете немного больше о действительных числах и некоторых их подмножествах, мы можем перейти к обсуждению некоторых свойств действительных чисел (и операций над действительными числами). Хотя некоторые свойства очевидны, они, тем не менее, полезны для обоснования различных шагов, необходимых для решения задач или доказательства теорем. Помните: переменные — это просто неизвестные значения, поэтому они действуют так же, как числа, когда вы складываете, вычитаете, умножаете, делите и т. д.
д.
Одним из свойств является то, что умножение и сложение действительных чисел являются коммутативными. Коммутативность утверждает, что порядок умножения или сложения двух чисел не влияет на результат. Мы можем записать это символически ниже, где x и y — два действительных числа (обратите внимание, что . можно использовать вместо для обозначения умножения):
Представьте, что у вас есть группа из x бананов и группа из y бананов; не имеет значения, как вы их сложите, общее количество бананов всегда будет одинаковым: либо x + y , либо y + x . Точно так же, если у вас есть прямоугольник с длиной x и шириной y , не имеет значения, умножаете ли вы x на y или y на x 9.0275 ; площадь прямоугольника всегда одинакова, как показано ниже.
Другим свойством, подобным коммутативности, является ассоциативность. Ассоциативность указывает, что порядок сложения трех чисел или порядок их умножения не влияет на результат. Если рассматривать действительные числа x , y и z , то
Ассоциативность указывает, что порядок сложения трех чисел или порядок их умножения не влияет на результат. Если рассматривать действительные числа x , y и z , то
Напомним, что операции в скобках выполняются перед теми, что вне скобок.
Распределяемость — еще одно свойство действительных чисел, которое в данном случае относится к комбинации умножения и сложения. Это свойство выражено ниже.
Мы можем понять это свойство, снова взглянув на группы бананов. Предположим, например, что у нас есть 3 группы по 6 бананов и 3 группы по 5 бананов. Если мы объединим эти группы один к одному (одна группа из 6 бананов с одной группой из 5), мы получим 3 группы по 11 бананов.
Последние два свойства, которые мы обсудим, — тождественность и инверсия. Свойство identity просто утверждает, что сложение любого числа x с 0 дает просто x , а умножение любого числа x на 1 равно x .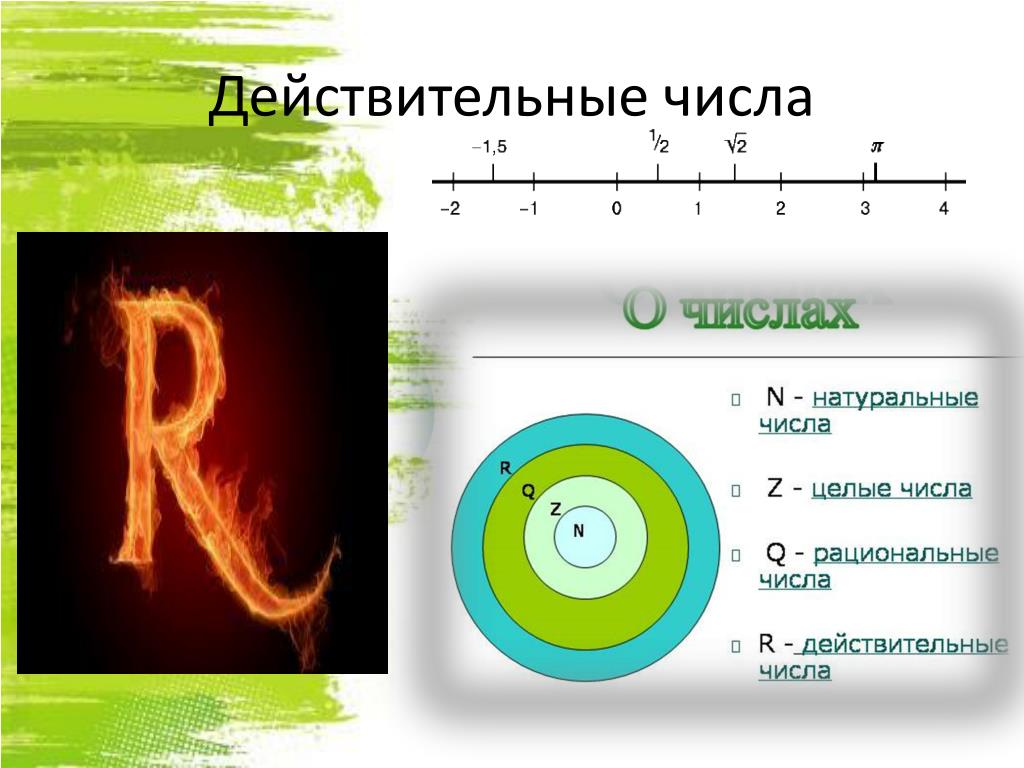
Свойство числа инвертирует для действительного числа x
и утверждает следующее:0003
Обратите внимание, что обратное свойство тесно связано с тождеством.
Эти свойства сами по себе могут показаться немного эзотерическими. Хотя, если их полностью вырвать из контекста, они могут показаться менее чем полезными, оказывается, что вы будете использовать их регулярно, даже если вы явно не признаете это в каждом случае.
Практическая задача: Определите свойство действительных чисел, которое оправдывает каждое равенство:
a + i = i + a ; ; 5 r + 3 s — (5 r + 3 s ) = 0.
Solution: In the first case, a + i = i + a , равенство явно подтверждается коммутативностью.