Содержание
Поддерживаемые форматы обозначений—ArcGIS Pro | Документация
В ArcGIS Desktop поддерживается ряд форматов чтения и записи местоположений координат из текстовой строки. Координаты с форматированным обозначением можно использовать в инструментах геообработки, например в инструменте Конвертировать обозначения координат.
В примерах и пояснениях ниже используется следующий синтаксис:
- | означает «или». Например, + | — означает, что можно использовать либо символ + либо -.
- [ ] обозначает список выбора. Например, [ + | — | N | S] означает, что можно использовать символы +, -, N либо S.
- < > обозначает значение.
Локализация для десятичных символов или аббревиатур полушария. Например, для выражения десятичных значений можно использовать только точку, но не запятую. Для обозначения полушарий используются только символы N, S, E и W, но не соответствующим им буквы других языков.
Форматы, использующие градусы
Для форматов, использующие градусы, первым всегда указывается значение широты (координата Y), затем значение долготы (координата X). Задайте полушарие с помощью обозначений +,-,N,S,E или W. Их можно смешивать в одной паре координат широта-долгота. Если они не указаны, значение считается положительным (N для широты или E для долготы).
DD (десятичные градусы)
Входной формат
<широта> <разделитель_пары_координат> <долгота>
широта | [ + | — | N | S ] <DD.dd> [ + | — | N | S ] | Регистр не учитывается |
долгота | [ + | — | E | W ] <DDD.dd> [ + | — | E | W ] | Регистр не учитывается |
разделитель_пары_координат | [space | / | \ | | | , ] | Может использоваться несколько разделителей, например, запятая и пробел, два пробела |
Значения <DD. (U+005E)
(U+005E)
Тильда ~ (U007e)
Звездочка * (U+002A)
Знак градуса может не указываться.
Общая длина значения не может превышать 64 символа (включая конечный символ NULL).
Примеры ввода
Все следующие примеры ввода являются равноценными:
27.00N 087.00W27.00n 087.00w27.00N 087W+27.00 087W27N -87N27.00 W08727.00N/87W27.00N/87W27.00°N 087.00°W
Выходной формат
При записи обозначения десятичного градуса добавляются начальные нули и используются буквы для обозначения полушария.
Пример результата
Этот выходной формат используется ArcGIS по умолчанию.
27.00N 087.00W 27.00000N 087.00000W
DDM (градусы — минуты)
Нельзя указывать несколько знаков +/- signs в формате DD MM.mmm.
Входной формат
<широта> <разделитель_пары_координат> <долгота>
широта | [ + | — | N | S ] <DD MM. | Регистр не учитывается |
долгота | [ + | — | E | W ] <DDD MM.mmm> [ + | — | E | W ] | Регистр не учитывается |
разделитель_пары_координат | [space | / | \ | | | , ] | Может использоваться несколько разделителей, например, запятая и пробел, два пробела |
Значения широты <DDD MM.mmm> и долготы <DD MM.mmm> могут указываться в следующем формате:
<градусы> [<знак_градуса>] [<разделитель>] <минуты> [<десятичный знак>] <доля минуты> [<знак_минуты>]
градусы | 0 – 90 (широта) От 0 до +180 и от 0 до -180 (долгота) |
знак_градуса | Знак градуса ° (U+00B0) Кольцо над ° (U+02DA) Порядковый указатель в муж. Тильда ~ (U007e) Звездочка * (U+002A) |
разделитель | [ пробел | нижнее подчеркивание | дефис] |
минуты | от 0 до 59 |
десятичное | . |
доля минуты | знаки |
знак_минуты | Знак минуты ‘ (U+2032) Апостроф ‘ (U+0027) |
Знаки градуса и минуты могут не указываться.
Общая длина строкового значения не может превышать 64 символа (включая конечный символ NULL).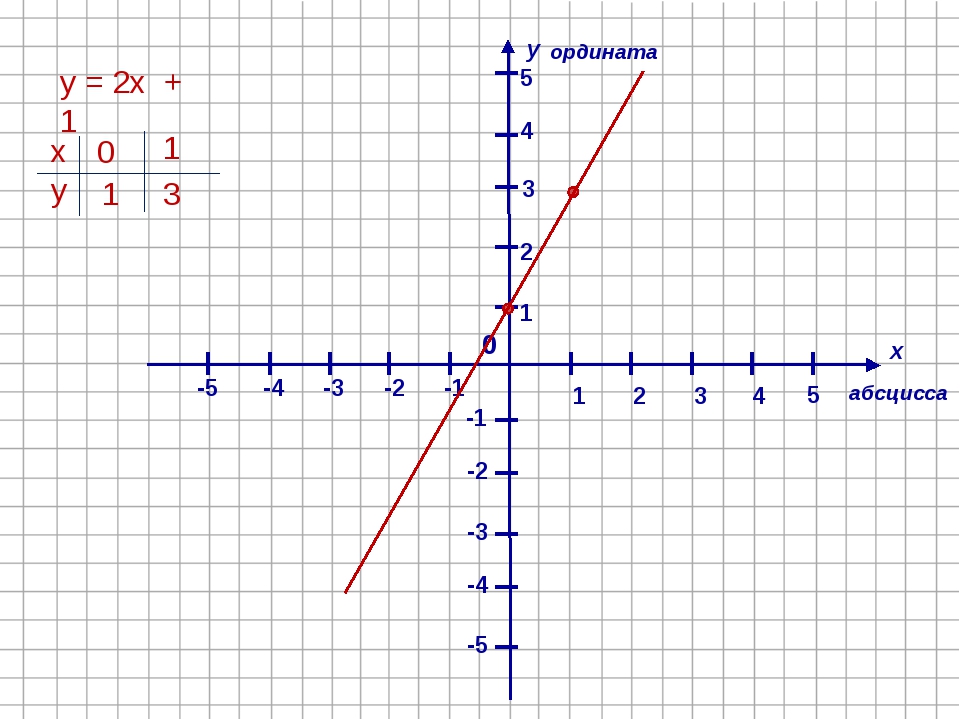
Примеры ввода
Все следующие примеры ввода являются равноценными:
27 54.00N 087 59.00W27 54.00n 087 59.00w27 54N 087 0W+27 54.00 087 59.00WN27 54.00 W087 59.0027 54.00N/87 59W27° 54.00’N 087° 59.00’W
Пример результата
Этот стандартный выходной формат используется ArcGIS по умолчанию.
27.00N 087.00W27 00.00000N 087 00.00000W
DMS (градусы-минуты-секунды)
Нельзя указывать несколько знаков +/- signs в формате DD MM SS.sss.
Входной формат
<широта> <разделитель_пары_координат> <долгота>
широта | [ + | — | N | S ] <DD MM SS.sss> [ + | — | N | S ] | Регистр не учитывается |
долгота | [ + | — | E | W ] <DDD MM SS. | Регистр не учитывается |
разделитель_пары_координат | [space | / | \ | | | , ] | Может использоваться несколько разделителей, например, запятая и пробел, два пробела |
Значения широты <DDD MM SS.sss> и долготы <DD MM SS.sss> могут указываться в следующем виде:
<градусы> [<знак_градуса>] <разделитель> <минуты> [<знак_минуты>] <разделитель> <секунды> [<десятичный знак>] <доля секунды> [<знак_секунды>]
градусы | 0 – 90 (широта) От 0 до +180 и от 0 до -180 (долгота) |
знак_градуса | Знак градуса ° (U+00B0) Кольцо над ° (U+02DA) Порядковый указатель в муж. Тильда ~ (U007e) Звездочка * (U+002A) |
разделитель | [ пробел | нижнее подчеркивание | дефис] |
минуты | от 0 до 59 |
знак_минуты | Знак минуты ‘ (U+2032) Апостроф ‘ (U+0027) |
секунды | от 0 до 59 |
десятичное | «.» |
доля секунды | знаки |
знак_секунды | Кавычка » (U+0022) Трема ¨ (U+00A8) Двойной акут ˝ (U+02DD) |
Знаки градуса, минуты и секунды могут не указываться.
Общая длина строкового значения не может превышать 64 символа (включая конечный символ NULL).
Примеры ввода
Все следующие примеры ввода являются равноценными:
27 18 00.00N 087 00 00.00W271800.00N 0870000.00W
Также поддерживается компактный формат DDMMSS.sss.
Пример результата
Этот стандартный выходной формат используется ArcGIS по умолчанию.
27 18 00.00N 087 00 00.00W
Универсальная поперечная проекция Меркатора (UTM)
При использовании обозначений UTM указывается зона и буква. Буква обычно представляет канал широты как в MGRS/USNG. В отдельных случаях могут использоваться буквы N или S для обозначения зоны UTM «Север» или «Юг». В смешанном списке всегда считается, что обозначения UTM использует канал широты.
Если обозначение UTM представлено строкой, не содержащей пробелов, часть строки, относящаяся к сдвигу на восток и на север разбивается на две половины. Если указано нечетное количество символов, лишний символ относится к части сдвига на север. Значения сдвига на восток и на север должны быть целыми числами.
Значения сдвига на восток и на север должны быть целыми числами.
11S3455674321459 = 11S 345567 4321459
11N345567432145 = 11N 345567 432145
Внимание:
Если обозначение UTM не содержит встроенных пробелов, четное количество символов может привести к противоречию. Например, сдвиг на восток должен содержать пять знаков, а сдвиг на север — семь, однако, программное обеспечение интерпретирует оба эти значения как содержащие шесть символов.
Если значение содержит встроенные пробелы, значения сдвига на восток и на север предположительно будут разделены пробелом и могут дополнительно содержать десятичные точки
Этот формат не поддерживается:
11S 3455674321459
при наличии запятой должен использовать строковый формат Easting,Northing,ZoneBand.
554577,4183342,10S
Допускается использование десятичных запятых. Пробелы в формате такого типа игнорируются.
554577.3,4183342.7,10S
Примеры ввода
Все следующие примеры ввода являются равноценными:
11S 345567 432145911S3455674321459554577,4183342,10S554577.3,4183342.7,10S554577, 4183342, 10S
Пример результата
11T 561192 4832027
Военная система прямоугольных координат (MGRS)
ZZBGGEEEEENNNNN
- ZZ: зона UTM
- B: канал широты
- GG: буквы, обозначающие площадь сетки 100 K (универсальная полярная стереографическая проекция для полярных регионов)
- EEEEE: координата X (сдвиг на восток)
- NNNNN: координата Y (сдвиг на север)
Сочетание первых трех букв ZZB иногда называют «Обозначение фрагмента сетки».
Использование пробелов допускается во входных данных, но не между значениями сдвига на восток и на север. После значений сдвига на восток указываются значения сдвига на север. Количество знаков, используемых для значений сдвига на восток и сдвига на север, должно совпадать.
Координаты MGRS можно округлить для меньшей точности. Пример:
- 15SWC8081751205 указывается с точностью до 1 метра.

- 15SWC80825121 указывается с точностью до 10 метров.
- 15SWC808512 указывается с точностью до 100 метров.
- 15SWC8151 указывается с точностью до 1000 метров.
В зависимости от датума или эллипсоида для MGRS будет использован новый или старый стиль. Старый стиль использует альтернативную схему присвоения букв. USNG (упрощенная версия MGRS) использует только новый формат, даже если он основывается на датуме NAD 1927, при использовании которого в MGRS применяется старый стиль. В целом одна из схем используется для WGS 1984 и NAD 1983, а вторая – для более ранних эллипсоидов, связанная с локальными датумами. Например, эта координата указана в формате WGS 1984:
15SWC8081751205
При ее преобразовании в схему датума NAD-27 datum, эллипсоид Clarke 1866, присваивается следующее значение:
15SWN8083350993
Универсальная полярная стереографическая проекция (UPS) разделает антарктический регион на зоны A и B, а арктический регион — на зоны Y и Z. Номера зонам не присваиваются.
Номера зонам не присваиваются.
ZAK4500045522 = 169 36 50.2E 87 45 7.2N = (169.6139E 87.7520N)
ZGG7902863771 = 85:40:30.0 N 85:40:30.0 W
ATN2097136228 = 85:40:30.0 S 85:40:30.0 W
Примеры ввода
Все следующие примеры ввода являются равноценными:
15SWC808175120515S WC 8081751205ZAK4500045522
Пример результата
По стандарту использование пробелов в выходных данных не допускается.
15SWC8081751205ZAK4500045522
United States National Grid (USNG)
Схема обозначения координат в системе USNG представляет собой упрощенную версию MGRS на основе национальной энергосистемы США.
Дополнительные сведения см. в разделе Стандарт United States National Grid, FGDC-STD-011-2001.
USNG поддерживает только две географические системы координат: NAD 1983 (эквивалентна WGS 1984) и NAD 1927. USNG по умолчанию использует NAD 1983. При использовании системы NAD27 необходимо явно задать ее, например: 18SUJ2306 (NAD 27). В отличие от MGRS, USNG использует ту же схему присвоения букв для своих 100 км квадратов независимо от используемой системы географических координат. MGRS сдвигает северную букву на 10 знаков при использовании старого стиля с NAD 1927. Таким образом, MGRS и USNG, основанные на NAD 1927, нельзя включить в смешанный список обозначений.
При использовании системы NAD27 необходимо явно задать ее, например: 18SUJ2306 (NAD 27). В отличие от MGRS, USNG использует ту же схему присвоения букв для своих 100 км квадратов независимо от используемой системы географических координат. MGRS сдвигает северную букву на 10 знаков при использовании старого стиля с NAD 1927. Таким образом, MGRS и USNG, основанные на NAD 1927, нельзя включить в смешанный список обозначений.
В отличие от MGRS в USNG допускается использование пробелов, например 18T WL 807 046.
Система USNG применяется только для территории США, включая внешние владения и территории. Координаты MGRS определяются для всей карты мира – в диапазоне значений широты между 80°S и 84°N определение выполняется средствами UTM, однако, вне этого диапазона координаты определяются в рамках универсальной полярной стереографической проекции (UPS). Из-за ограничений диапазона USNG не требует использования UPS и определяется исключительно средствами UTM.
Примеры ввода
Все следующие примеры ввода являются равноценными:
11SMT824647520711S MT 82464 75207
Пример результата
11S MT 82464 75207
Всемирная система географических координат (GEOREF)
Система GEOREF основана на координатах долготы и широты. Карта мира разделяется сначала на ячейки 15х15 градусов, которые помечены буквами. Каждая из этих ячеек затем подразделяется на ячейки 1х1 градус, также с буквенным обозначением. Каждая из ячеек 1х1 градус может быть разделена на ячейки 60х60 минут, как показано в примере ниже. Дальнейшие деления допускаются до 0,01 минуты.
Карта мира разделяется сначала на ячейки 15х15 градусов, которые помечены буквами. Каждая из этих ячеек затем подразделяется на ячейки 1х1 градус, также с буквенным обозначением. Каждая из ячеек 1х1 градус может быть разделена на ячейки 60х60 минут, как показано в примере ниже. Дальнейшие деления допускаются до 0,01 минуты.
Пример ввода
PGAM16281221
Пример результата
PGAM1628
Global Area Reference System (GARS)
Система GARS основана на координатах широты и долготы. Карты мира подразделяется на ячейки 30х30 минут. Первые три символа представляют полосу долготы шириной 30 минут. Четвертый и пятый символы представляют полосу долготы высотой 30 минут. Каждую из ячеек 30х30 минут можно разделить на четыре ячейки 15х15 минут, и каждую из них – на девять ячеек 5х5 минут. При преобразовании из GARS нижний левый угол представленного квадрата используется для вычисления координат в градусах.
Примеры ввода
391JL41391JL
Пример результата
391JL41
Смешанные форматы обозначений
В отношении преобразования набора смешанных строковых обозначений действуют следующие условия. Эффективное определение некоторых форматов обозначения невозможно.
Эффективное определение некоторых форматов обозначения невозможно.
Все списки смешанных форматов обозначений должны использовать одинаковую систему географических координат (датум). Система GCS не задана явно, WGS 1984 подразумевается.
В зависимости от датума или эллипсоида для MGRS будет использован новый или старый стиль. Старый стиль использует альтернативную схему присвоения букв. USNG (упрощенная версия MGRS) использует только новый формат, даже если он основывается на датуме NAD 1927, при использовании которого в MGRS применяется старый стиль. Если строковые обозначения и MGRS, и USNG, использующие систему NAD 1927, находятся в одном списке, корректное преобразование в другой тип координат или обозначений невозможно.
При использовании обозначений UTM указывается зона и буква. Буква обычно представляет канал широты как в MGRS/USNG. В отдельных случаях могут использоваться буквы N или S для обозначения зоны UTM «Север» или «Юг». В смешанном списке всегда считается, что обозначения UTM использует канал широты.
Координаты GARS должны располагаться слева внизу (не в центре).
Формат DD.MMSSsss не поддерживается (возможно противоречие с DD.dddddd или DD.MMmmm).
При указании всех обозначений в градусах (например, DD.dddd, DDMM.mmmm, DDMMSS.ssss или DD MM SS.ssss) значения широты и долготы должны указываться в одинаковом формат.
Можно комбинировать +/- или NSEW, но эти обозначения следует указывать в начале или конце значения (dd mm ss.ssss-).
Нельзя указывать несколько знаков +/- signs в формате DD MM.mmm или DD MM SS.ssss.
Отзыв по этому разделу?
Как найти Координаты Точки? Примеры
Поможем понять и полюбить математику
Начать учиться
114.7K
Современные технологии позволяют в несколько кликов поделиться с другом нашим месторасположением. Достаточно зайти в гугл карты и пошерить координаты точки. В этом материале узнаем, как такое же действие отобразить на бумаге.
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
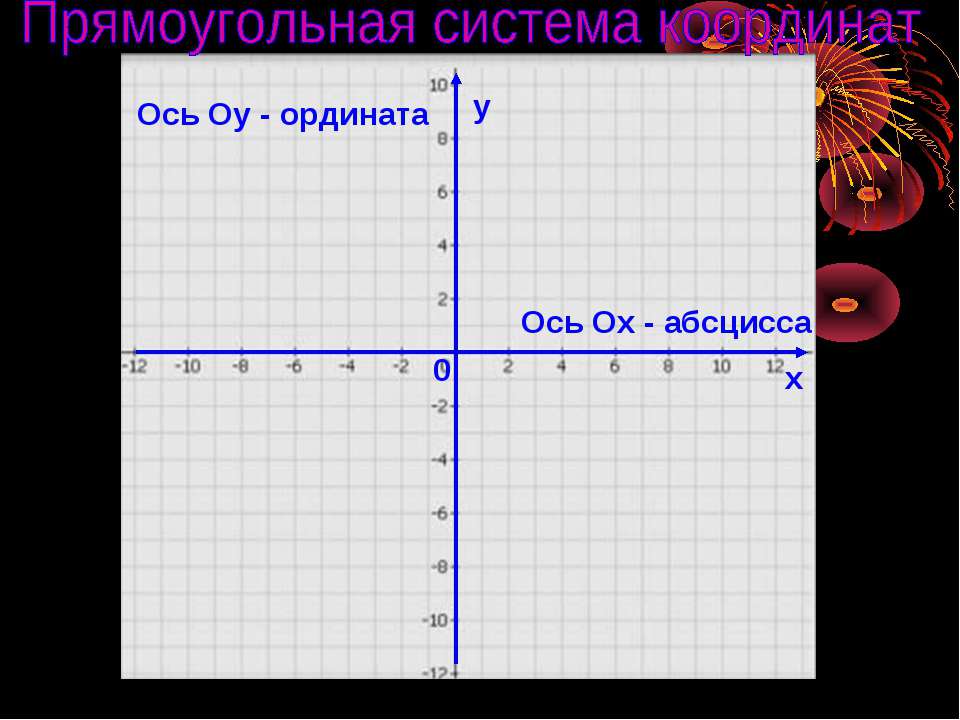
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат.
 Обозначается так: x0y.
Обозначается так: x0y. - Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
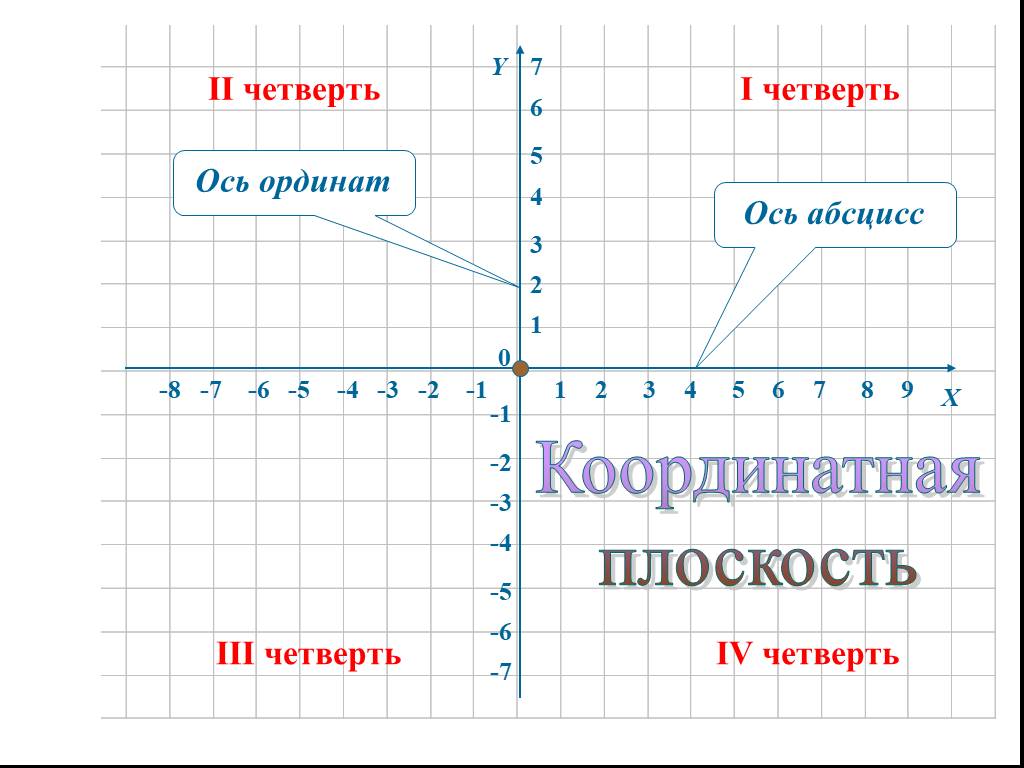
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Правила координат:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.

- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.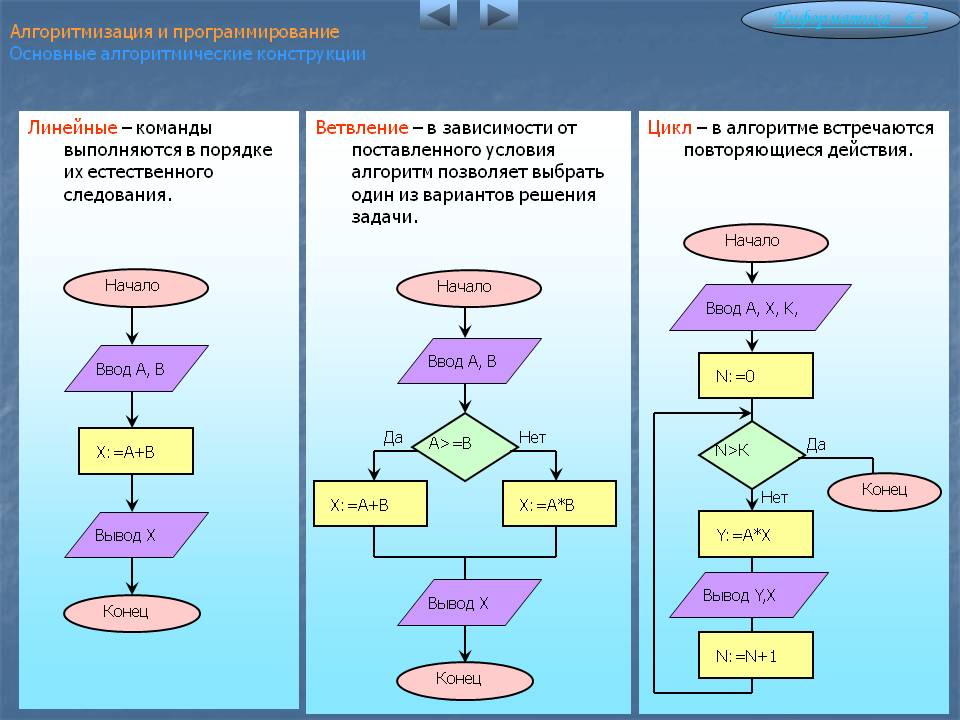
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.

- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
- Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
139.9K
Что такое функция?
К следующей статье
Как умножать отрицательные числа
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Что такое координаты x и y?
К
- Рахул Авати
Что такое координаты x и y?
Координаты X и y — это, соответственно, горизонтальный и вертикальный адреса точки в любом двумерном (2D) пространстве, таком как лист бумаги или экран дисплея компьютера. Вместе эти координаты помогают определить точное местоположение точки.
Вместе эти координаты помогают определить точное местоположение точки.
В декартовой системе координат координаты x и y являются частью осей x и y в 2D-пространстве. Для точки в пространстве координаты x и y записываются в виде упорядоченной пары (x, y). Первое число представляет положение точки на оси x, а второе число представляет ее положение на оси y. Координаты также могут быть записаны как (x,y) без пробела после запятой.
Координаты X и Y (оси) — это горизонтальные и вертикальные адреса в 2D-пространстве.
Порядок координат x и y в упорядоченной паре важен. Координата x всегда идет первой, за ней следует координата y. Вот почему (3, 4) не то же самое, что (4, 3).
(3, 4) относится к точке на три единицы справа от нуля и на четыре единицы выше нуля.
(4, 3) относится к точке на четыре единицы справа от нуля и на три единицы выше нуля.
Две оси пересекаются перпендикулярно в исходной или нулевой точке. Координаты x и y этого местоположения записываются как (0, 0) или (0,0).
Важные координаты x и y
Оси x и y, на которых нанесены координаты x и y, образуют координатную плоскость. Система была изобретена французским математиком Рене Декартом и известна как декартова система координат.
Координатная плоскость необходима для представления любой точки в заданном 2D-пространстве. Плоскость, образованная пересечением двух осей, является двумерной, поскольку для определения положения любой точки на этой плоскости требуются две точки данных:
- его расстояние по оси x
- его расстояние по оси Y
Эти расстояния представлены координатой x и координатой y соответственно.
Значение x точки (x, y) известно как абсцисса . Он представляет собой расстояние точки от начала координат или вдоль горизонтальной оси X. Значение y точки (x, y) известно как ордината . Он представляет собой вертикальное или перпендикулярное расстояние точки от начала координат или от оси x.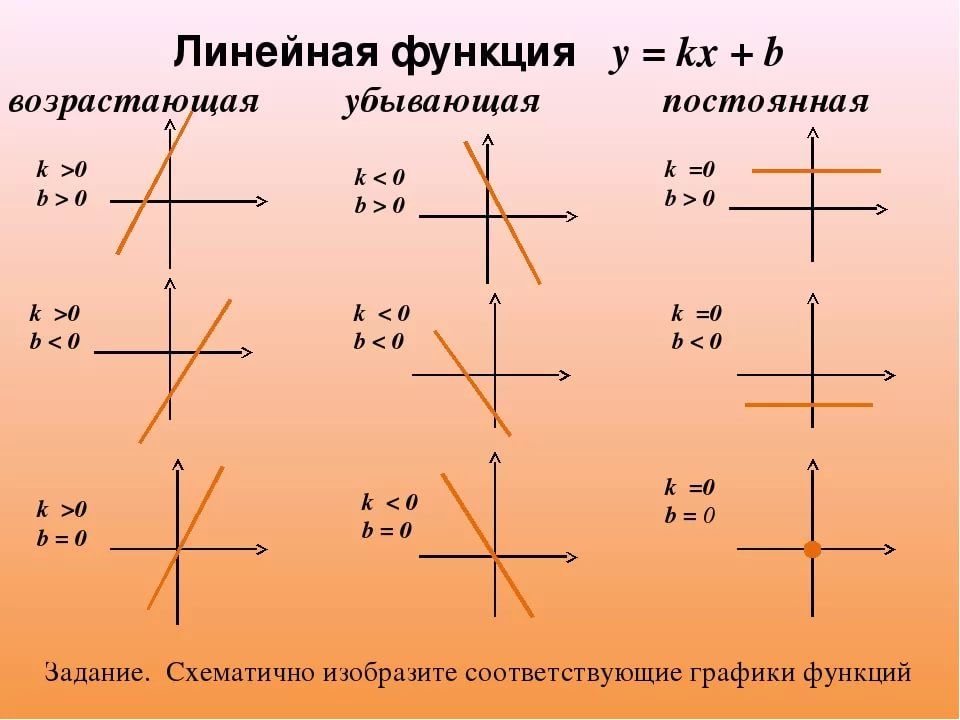
Точка, в которой линия пересекает ось x, называется x- точкой пересечения , а точка, в которой она пересекает ось y, называется точкой пересечения y . Координата y точки пересечения x равна 0, а координата x точки пересечения y равна 0. Если доступно уравнение прямой (y = mx + b), подстановка x = 0 в уравнение дает y -перехват. Точно так же подстановка y = 0 дает точку пересечения по оси x.
Координатная плоскость разделена на четыре квадранта:
- Квадрант 1 находится вверху справа.
- Квадрант 2 находится вверху слева.
- Квадрант 3 находится внизу слева.
- Квадрант 4 находится внизу справа.
Представление координат x и y с примерами
Любая точка в двумерном пространстве представлена координатами x и y в виде упорядоченной пары, любая из которых может быть нулевой, положительной или отрицательной.
Если одно из значений равно нулю, точка представляется следующим образом:
- (0, y): координата x равна нулю, поэтому точка лежит на оси y.

- (0, 10): точка находится на оси Y и на 10 единиц выше .
- (0, -10): точка находится на оси Y и на 10 единиц ниже .
- (x, 0): координата y равна нулю, поэтому точка лежит на оси x.
- (10, 0): точка находится на оси X и на 10 единиц вправо от нуля.
- (-10, 0): точка находится на оси х и 10 единицах к осталось нулей.
Если обе координаты x и y равны нулю (0, 0), точка находится в начале координат, где оси x и y пересекаются.
Если обе координаты x и y отличны от нуля, точка находится где-то на двумерной координатной плоскости в одном из ее четырех квадрантов.
Пример 1
Здесь рассмотрим точку M в координатной плоскости.
М лежит на одну единицу правее нуля и на две единицы выше нуля. Таким образом, его координата x равна (1), а его координата y равна (2). Вместе его координаты (x, y) представлены на двухмерной координатной плоскости следующим образом:
М = (1, 2)
Точка M находится в квадранте 1.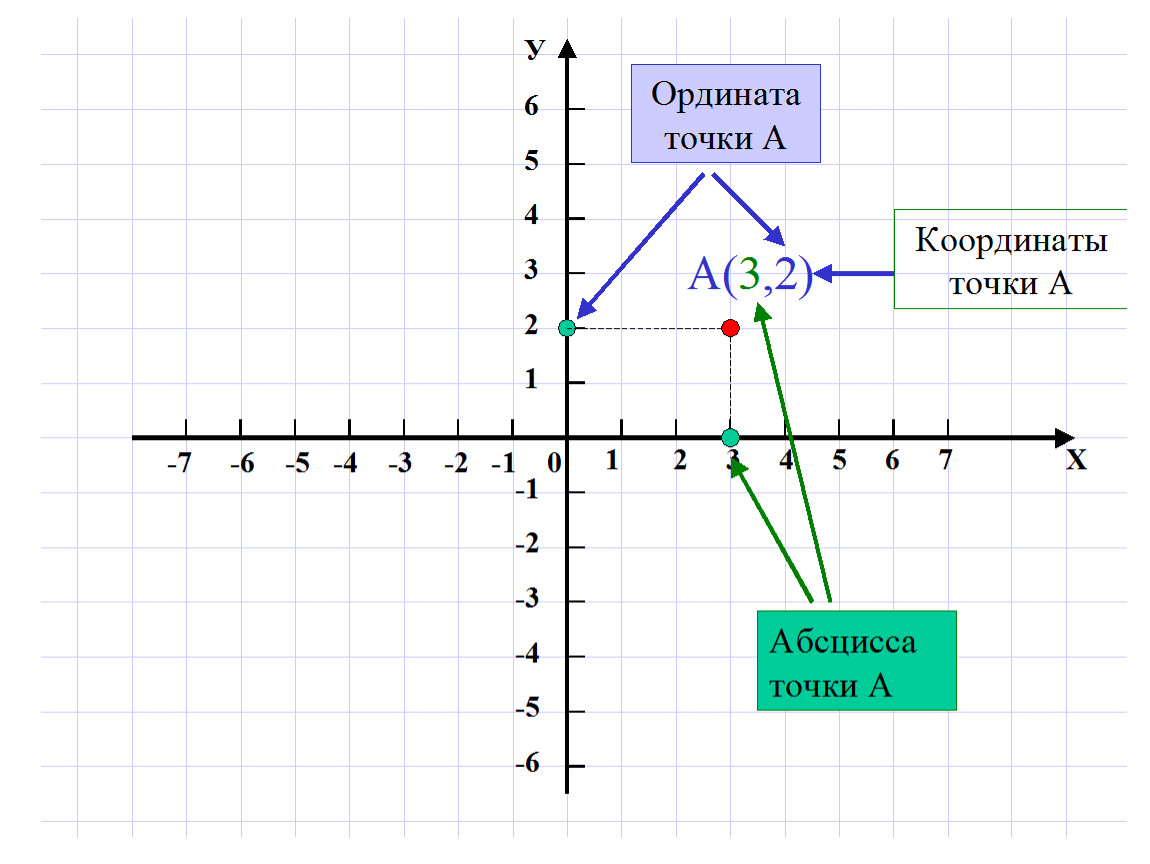
Пример 2
Здесь рассмотрим точку N в координатной плоскости.
N лежит на три единицы левее нуля и на четыре единицы ниже нуля. Итак, его координата x равна (-3), а координата y равна (-4). Вместе его координаты (x, y) представлены на двухмерной координатной плоскости следующим образом:
Н = (-3, -4)
Точка N находится в квадранте 3.
Положительные и отрицательные значения в 4 квадрантах
В зависимости от положения точки в одном из четырех квадрантов координатной плоскости координаты x и y будут иметь положительные или отрицательные значения. Если координата x находится в левой части плоскости, она имеет отрицательное значение, а если в правой, то ее значение положительное.
Аналогично, если координата y находится в верхней части плоскости, ее значение положительно. Если он находится в нижней плоскости, он имеет отрицательное значение. Левая, правая, верхняя и нижняя части плоскости определяются положением точки от начала координат или нулевого значения.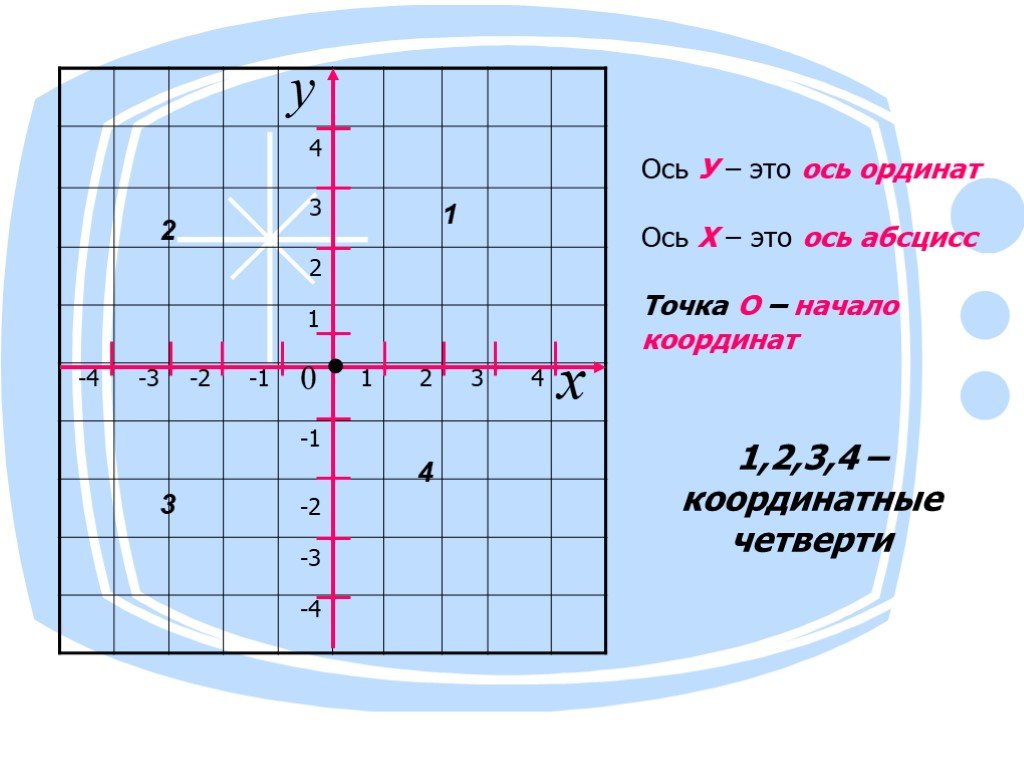
| Квадрант | Местоположение точки | Значение X (положительное/отрицательное) | Значение Y (положительное/отрицательное) | (х, у) |
Квадрант 1 | Вверху справа | Положительный | Положительный | (+, +) |
Квадрант 2 | Вверху слева | Отрицательный | Положительный | (-, +) |
Квадрант 3 | Внизу слева | Отрицательный | Отрицательный | (-, -) |
Квадрант 4 | Внизу справа | Положительный | Отрицательный | (+, -) |
Пример 1
(2, 5): точка находится в квадранте 1, на две единицы вправо от нуля и на пять единиц выше нуля.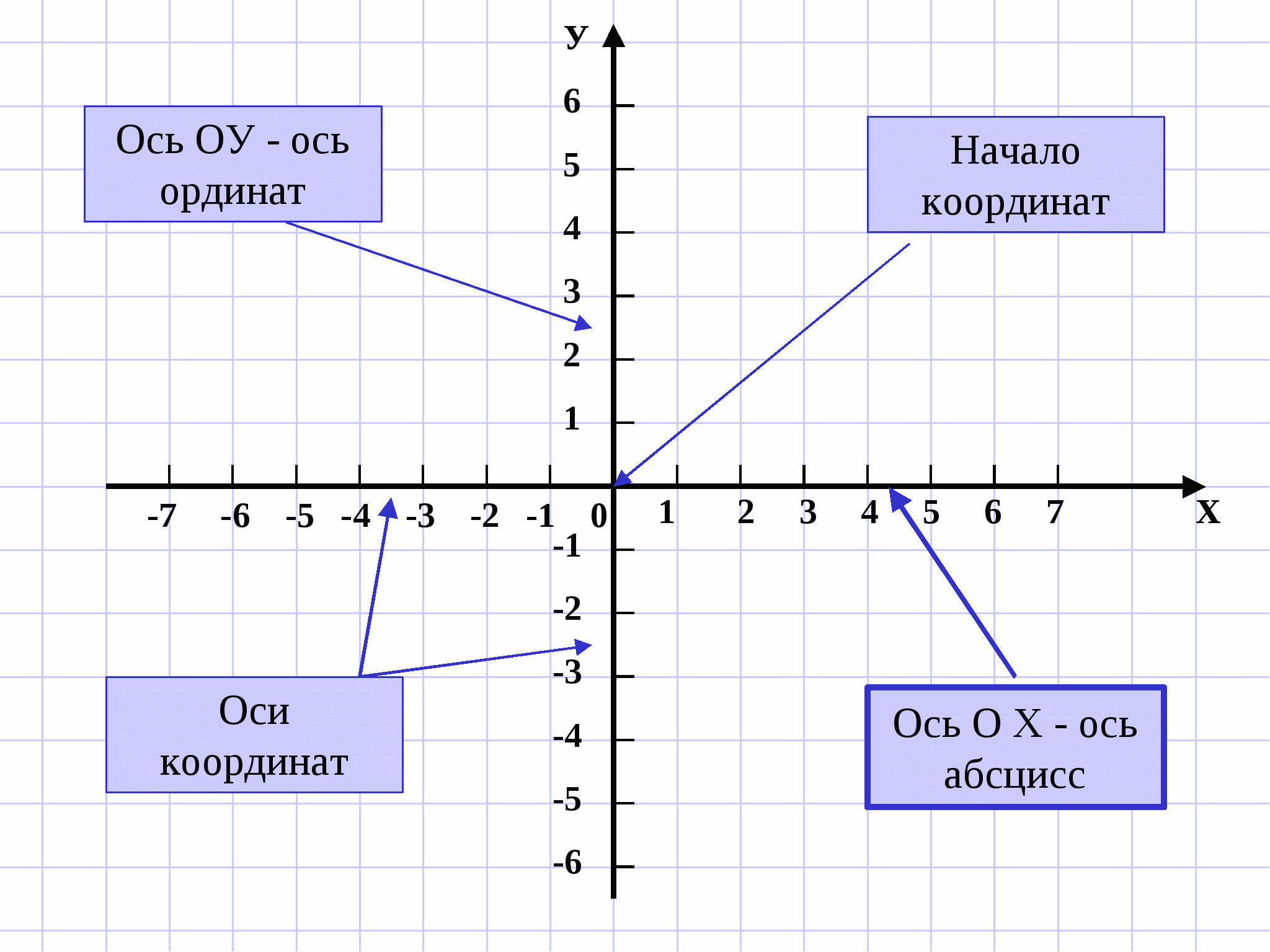
Пример 2
(-2, 5): точка находится в квадранте 2, две единицы до осталось нуля и пять единиц выше нуля.
Пример 3
(-2, -5): точка находится в квадранте 3, две единицы до слева от нуля и пять единиц ниже нуля.
Пример 4
(2, -5): точка находится в квадранте 4, на две единицы правее нуля и на пять единиц ниже нуля.
Использование координат x и y
Координаты x и y точки необходимы для определения расстояния этой точки от заявленного начала координат 2D-пространства. Координаты также используются для нахождения середины и наклона линии, а также для определения ее линейного уравнения.
Линейное уравнение прямой представляется как y = mx + b:
- м = уклон = изменение по у / изменение по х
- х = координата х, «как далеко»
- y = координата y, «как далеко вверх»
- b = значение y, когда x = 0
Вот как выглядит пара координат (x, y), если значение x известно и уравнение выражается как y = 2x + 2:
| Координата X | Координата Y | Уклон (м) | у = 2х + 2 | (х, у) |
0 | 2 | 2 | 2 | (0, 2) |
1 | 4 | 2 | 4 | (1, 4) |
2 | 6 | 2 | 6 | (2, 6) |
3 | 8 | 2 | 8 | (3, 8) |
4 | 10 | 2 | 10 | (4, 10) |
Чтобы изобразить уравнение y = 2x + 2, каждая координата в каждой упорядоченной паре расположена на координатной сетке.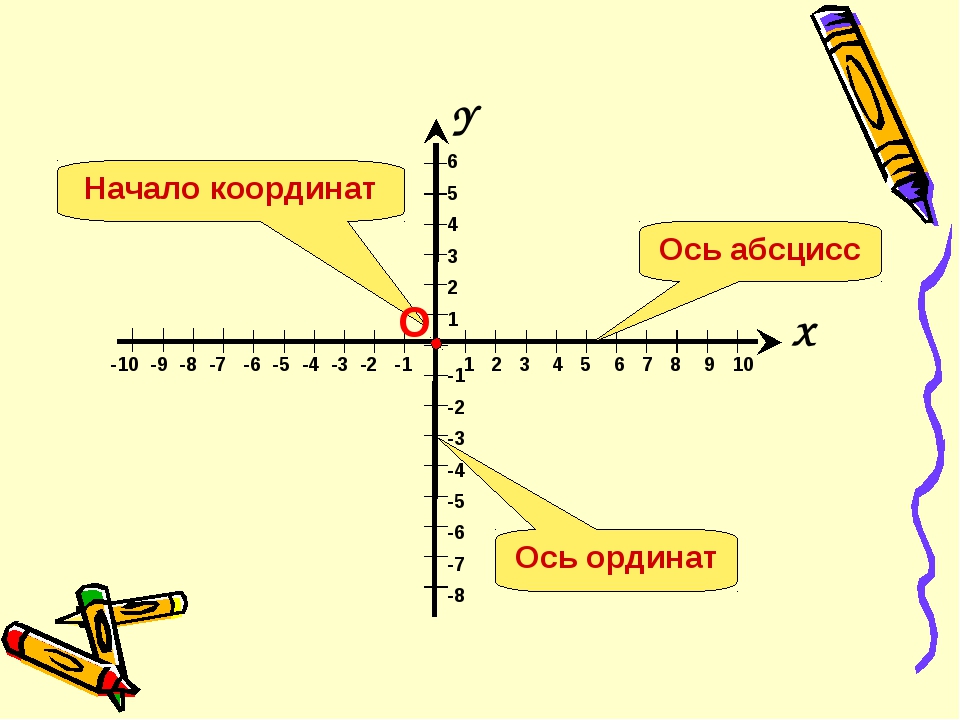 Затем координаты x и y соединяются в прямую линию.
Затем координаты x и y соединяются в прямую линию.
См. также: математические символы .
Последнее обновление: август 2022 г.
Продолжить чтение О координатах x и y
- Медицинская школа Kaiser Permanente для обучения студентов современным технологиям
- Как предприятия будут использовать еще не определенную метавселенную
- Чем CPU, GPU и DPU отличаются друг от друга?
- Как улучшение математических навыков может помочь в программировании
- Будущее науки о данных: карьерный рост и отраслевые тенденции
сторонний файл cookie
Сторонний файл cookie — это файл cookie, который размещается на устройстве пользователя — компьютере, мобильном телефоне или планшете — веб-сайтом из домена, отличного от того, который посещает пользователь.
Сеть
-
CAPWAP (Контроль и настройка точек беспроводного доступа)CAPWAP (управление и предоставление беспроводных точек доступа) — это протокол, который позволяет контроллеру доступа управлять .
 ..
.. -
мониторинг производительности сети (NPM)Мониторинг производительности сети (NPM) — это процесс измерения и мониторинга качества обслуживания сети.
-
инфракрасное излучение (ИК)Инфракрасное излучение (ИК), иногда называемое просто инфракрасным, представляет собой область спектра электромагнитного излучения, в которой …
Безопасность
-
NICE Framework (Национальная инициатива по обучению кибербезопасности Cybersecurity Workforce Framework)The NICE Framework (National Initiative for Cybersecurity Education Cybersecurity Workforce Framework) является справочным ресурсом …
-
черный список приложений (занесение приложений в черный список)Занесение приложений в черный список — все чаще называемое занесением в черный список приложений — представляет собой практику сетевого или компьютерного администрирования, используемую .
 ..
.. -
соковыжималкаJuice jacking — это эксплойт безопасности, в котором зараженная зарядная станция USB используется для компрометации устройств, которые к ней подключаются.
ИТ-директор
-
Общепринятые принципы ведения учета (Принципы)Общепринятые принципы ведения документации — это основа для управления записями таким образом, чтобы поддерживать …
-
система управления обучением (LMS)Система управления обучением представляет собой программное приложение или веб-технологию, используемую для планирования, реализации и оценки конкретных …
-
Информационный векИнформационная эпоха — это идея о том, что доступ к информации и контроль над ней являются определяющими характеристиками нынешней эпохи …
HRSoftware
-
конвейер талантовВоронка талантов — это группа кандидатов, готовых занять вакансию.

-
аутсорсинг процесса подбора персонала (RPO)Аутсорсинг процесса найма (RPO) — это когда работодатель передает ответственность за поиск потенциальных кандидатов на работу …
-
специалист по кадрам (HR)Специалист по персоналу — это специалист по кадрам, который выполняет повседневные обязанности по управлению талантами, сотрудникам …
Служба поддержки клиентов
-
управление маркетинговой кампаниейУправление маркетинговыми кампаниями — это планирование, выполнение, отслеживание и анализ кампаний прямого маркетинга.
-
ведущий специалист по продажам (SQL)Лид, квалифицированный по продажам (SQL), — это потенциальный клиент, который был изучен и проверен — сначала организацией …
-
Платформа Adobe ExperienceAdobe Experience Platform — это набор решений Adobe для управления качеством обслуживания клиентов (CXM).

Ось X и Y
Ось X и Y являются осями в декартовой системе координат. Вместе они образуют координатную плоскость, которая представляет собой пространство, в котором происходит двумерное графическое изображение.
В двумерном пространстве ось X является горизонтальной осью, а ось Y — вертикальной осью. Они представлены двумя числовыми линиями, которые пересекаются перпендикулярно в начале координат, расположенном в точке (0, 0), как показано на рисунке ниже.
Приведенное выше представление координатной плоскости является одной из самых основных форм, где каждая галочка на оси представляет собой 1 единицу. Стоит отметить, что оси могут быть помечены любым количеством способов, если каждая ось поддерживает постоянный интервал. Например, вместо того, чтобы ось X считала вверх на 1, первая отметка справа от 0 может быть помечена как 2, последующая — как 4, а следующая — как 6. В этом случае расстояние между каждой отметкой представляет собой 2.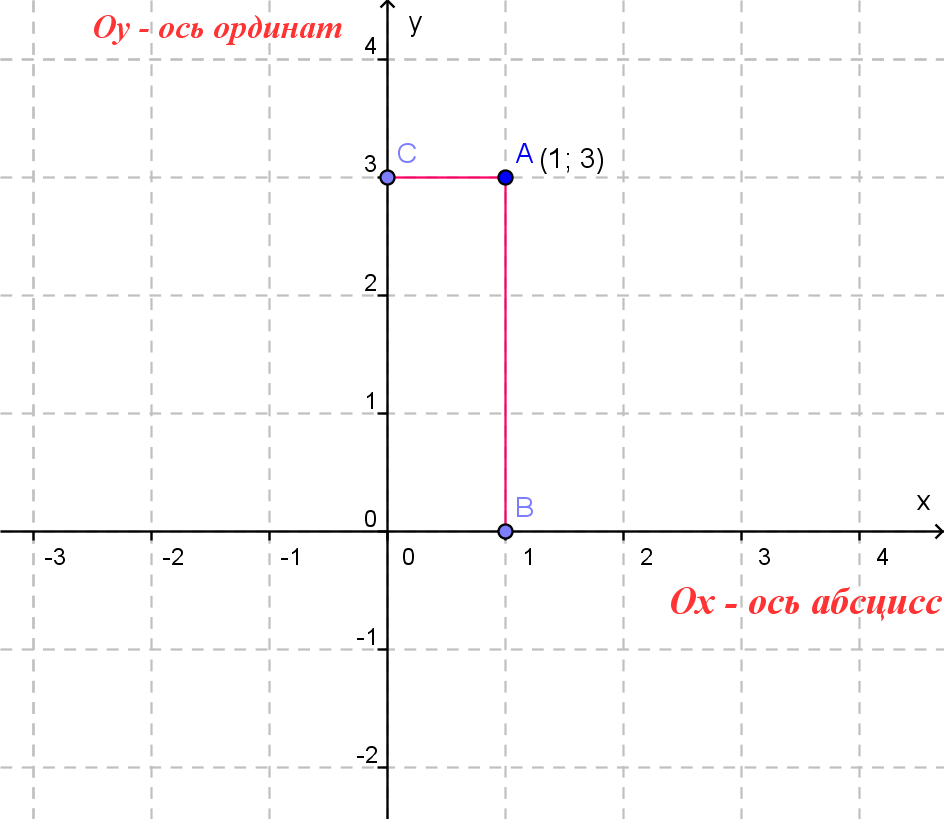 единицы измерения. Ось Y в этом же примере может даже иметь деления, представляющие 3 единицы; ось X и ось Y не должны иметь одинаковый интервал между метками. Поэтому важно обращать внимание на маркировку осей, поскольку различия в выбранных интервалах осей могут существенно повлиять на форму данного графика.
единицы измерения. Ось Y в этом же примере может даже иметь деления, представляющие 3 единицы; ось X и ось Y не должны иметь одинаковый интервал между метками. Поэтому важно обращать внимание на маркировку осей, поскольку различия в выбранных интервалах осей могут существенно повлиять на форму данного графика.
Упорядоченные пары
Заданная точка на координатной плоскости обозначается с помощью так называемой упорядоченной пары. Упорядоченная пара — это пара значений, в которой первое значение указывает координату x, а второе — координату y. Упорядоченная пара записывается следующим образом:
(x, y)
, где x — значение x, а y — значение y. В упорядоченной паре значения x и y заключены в круглые скобки и разделены запятой. Обратите внимание, что причина, по которой она называется упорядоченной парой, заключается в том, что сначала должно идти значение x, а затем значение y. Другими словами, (x, y) не то же самое, что (y, x). Рассмотрим точки A, B и C, нанесенные на координатную плоскость ниже.
Красные стрелки показывают, как мы движемся от начала координат к заданной точке координатной плоскости, как описано ниже.
- Для точки A переместитесь вправо на 3 единицы по оси x, чтобы получить координату x, равную 3, затем переместитесь на 4 единицы вверх по оси y, чтобы получить координату y, равную 4.
- Для точки B переместитесь на 4 единицы влево по оси x, чтобы получить координату x -4. Поскольку вертикальное расстояние для перемещения по оси Y отсутствует, координата Y равна 0,
- Для точки C переместитесь на 4 единицы вправо по оси x, чтобы получить координату x, равную 4, затем переместитесь на 4 единицы вниз по оси y, чтобы получить координату y, равную -4.
.
Таким образом, чтобы нанести точку на координатную плоскость, нам просто нужно знать упорядоченную пару. Затем мы можем нанести точку, посчитав соответствующее количество единиц по осям x и y. Как только мы научились рисовать точки на координатной плоскости, мы можем перейти к графическому изображению более сложных объектов, поскольку график прямой или какой-либо другой функции — это просто визуальное представление всех точек или упорядоченных пар, составляющих функцию.

 mmm> [ + | — | N | S ]
mmm> [ + | — | N | S ]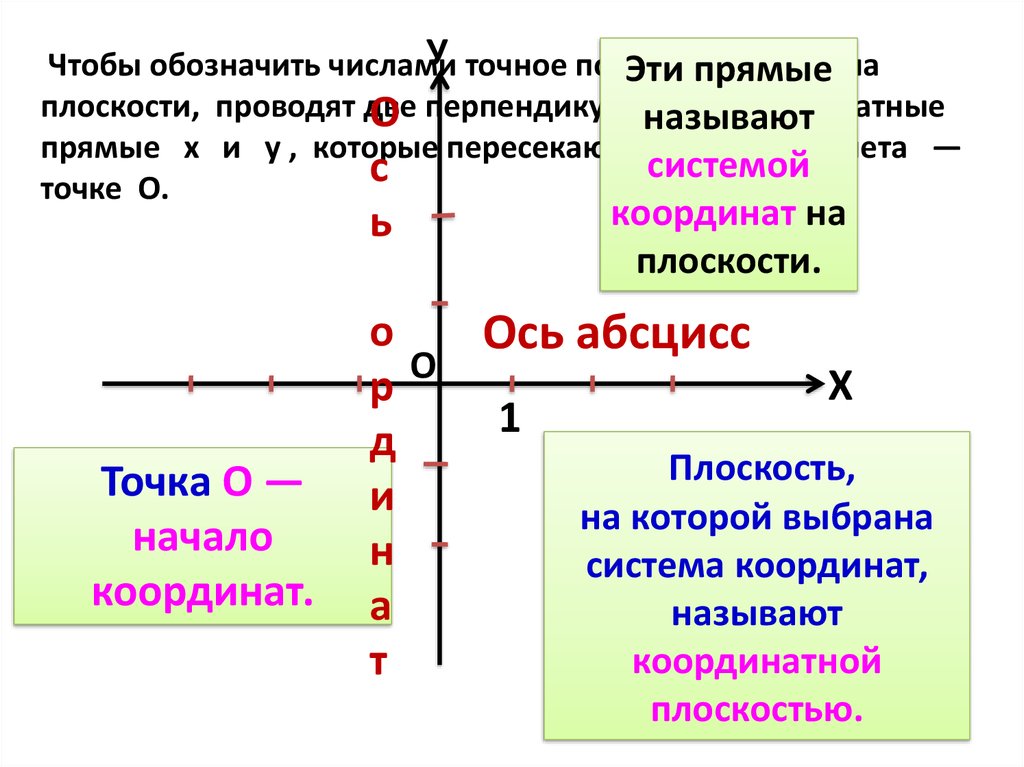 (U+005E)
(U+005E) sss> [ + | — | E | W ]
sss> [ + | — | E | W ] (U+005E)
(U+005E) 3,4183342.7,10S554577, 4183342, 10S
3,4183342.7,10S554577, 4183342, 10S
 Обозначается так: x0y.
Обозначается так: x0y.


 ..
.. ..
..