Применение кругов Эйлера к решению задач. В футбольной команде спартак 30 игроков среди них 18 нападающих
Life - Круги Эйлера.Решение задач.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
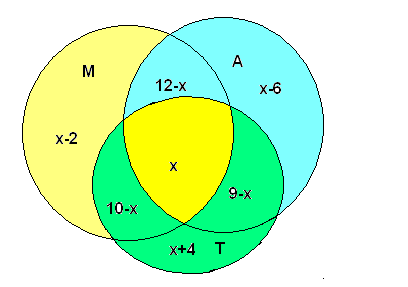
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро: 20 − (12 − х) − (10 − х) − х = х − 2 Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение: Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
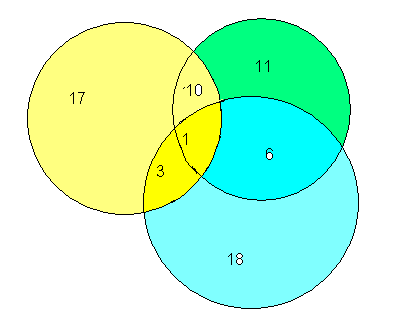
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.
Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
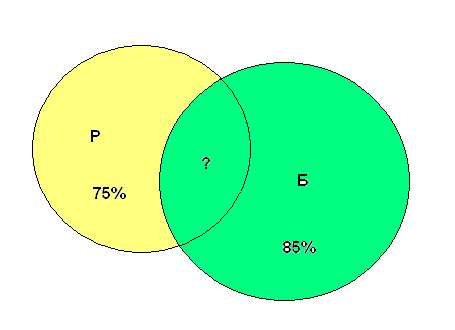В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%). Проект ученицы 9 класса "Круги Эйлера". Решение задач.
Проект
Тема:Круги Эйлера.
Выполнила: Нестеренко Марина
ученица 9б класса школы №367
«Школа надомного обучения
Научный руководитель:
учитель математики
Монакова Клара Захаровна
2010 г.
Оглавление.
1. Введение.
а) Исторические сведения.
б) Изображение множества чисел с помощью кругов Эйлера.
2. Решение задач с помощью кругов Эйлера.
а) Простые задачи.
б) Сложные задачи.
3. Заключение.
1. Введение.
Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N-множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.
Ну а как же круги Эйлера помогают при решении задач? Для ответа возьмем несколько задач:
2. Решение задач с помощью кругов Эйлера.
1. Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
Решение. Составим схему –
В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).
2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Решение. Обратимся к кругам Эйлера:
Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
3. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Решение.
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.
4. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Решение. 1 способ. Для решения опять воспользуемся кругами Эйлера:
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом:
20+15+23-10-12-9+х=30, 27+х=30, х=3.
5. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Решение
хотя бы 1
А + Н = 34 Ф + Н = 25
Н = 6
А + Н = на 3 человека >, чем Ф + Н = х
одновр. одновр.
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Всего 40 человек.
4. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и
холодильник и микроволновку, 19 - и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Решение:
Купили только холодильники: 35-(20-3)-(15-3)-3=4.
Купили только микроволновки: 36-(20-3)-(19-3)-3=0.
Купили только телевизоры: 37-(15-3)-(19-3)-3=6.
Тогда всего покупателей было: 4+17+3+16+12+6=58.
65-58=7 посетителей магазина не купили ничего.
Заключение.
В результате работы над данной темой я пришла к следующим выводам:
1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
2) Любое натуральное число является элементом любого следующего множества.
3) Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
nsportal.ru
Применение кругов Эйлера к решению задач
В спортивных соревнованиях участвует школьная команда из 20 человек, каждый из которых имеет спортивный разряд по одному или нескольким из трех видов спорта: легкой атлетике, плаванию и гимнастике. Известно, что 12 из них имеют разряды по легкой атлетике, 10 – по гимнастике и 5 – по плаванию. Сколько школьников из этой команды имеют разряды по всем видам спорта, если по легкой атлетике и плаванию разряды имеют 2 человека, по легкой атлетике и гимнастике – 4 человека, по плаванию и гимнастике – 2 человека?
В математике, когда какие-нибудь объекты собираются вместе говорят одно и то же слово – множество. Сказать «стадо чашек» нельзя, а множество чашек – можно. Сказать «бригада коров» нельзя, а множество коров – можно.
Предметы или живые существа, входящие во множество, называются элементами этого множества. Между множествами могут быть различные виды отношений. Для наглядной геометрической иллюстрации соотношений между множествами используются диаграммы Эйлера-Венна. Это замкнутая линия, внутри которой расположены элементы данного множества.
Леонард Эйлер (1707-1783) – крупнейший математик. Родившись в Базеле (Швейцария) в семье пастыря, Леонард получил первоначальное образование у своего отца. Отец предназначал сына к богословскому званию и определил его по окончании средней школы на теологический факультет. Однако Эйлер интересовался не теологией, а математикой, и стал слушать лекции известного профессора математики Иоганна Бернулли.
В 19 – летнем возрасте Эйлер опубликовал первую свою научную работу и принял участие в объявленном Парижской академией наук конкурсе на тему о наилучшем расположении мачт на корабле. В 1727 году Эйлер приехал в Петербург.
В Петербурге Эйлер нашел все необходимые условия для большой научной деятельности и широкие возможности для публикации своих трудов. Здесь он женился, провел большую часть творческого периода своей жизни, став главой первой русской математической школы, написал более 850 научных работ. В одной из них и появились круги.
Решая математические головоломки и развлекательные задачи, Эйлер заложил основы теории графов, ныне широко используемой во многих приложениях математики. Напряженная работа повлияла на зрение ученого. В 1735 году он ослеп на один глаз, а в 1766 на оба. Операция привела к незначительному улучшению: ученый мог лишь разбирать записи, сделанные мелом на черной доске. Но и после этого Эйлер продолжал работу, диктуя ученикам свои статьи.
Умер Эйлер в 76 лет и был похоронен на Смоленском кладбище Санкт-Петербурга. В 1957 году его прах был перенесен в Александро-Невскую лавру. Эйлер прожил в России 31 год. Многие дети и внуки остались жить в России, некоторые из его потомков поныне проживают в нашей стране.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Используется в математике, логике, менеджменте и других прикладных направлениях. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов, и они получили название «круги Эйлера».
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N -множество натуральных чисел, Z - множество целых чисел, Q - множество рациональных чисел, R - множество всех действительных чисел.
Общую часть множеств называют пересечением. Изображают так:Объединение множеств называют множество всех элементов, принадлежащих данным множествам.
А теперь вернемся к нашей задаче.
А-множество учащихся имеющих разряды по легкой атлетике.
В-множество учащихся имеющих разряды по плаванию.
С-множество учащихся имеющих разряды по гимнастики.
Нам надо найти, сколько элементов, то есть учащихся входят в пересечение множеств.
12 -2 = 10 - учащихся только по легкой атлетике.
10 -2 = 8 - учащихся только по плаванию.
5 -4 = 1 - учащихся только по гимнастике.
20-[(12-2)+(10-2)+(5-4)]=20-10-8-1=20-19=1 (уч. ) имеют разряд по всем видам спорта.
Задача 2
В классе можно изучать английский или французский язык. Известно, что английский язык изучают 20 школьников, а французский – 17. Всего в классе 32 ученика. Сколько учащихся изучают оба языка: и английский и французский
Решение.
А – изучают английский язык
В - изучают французский язык
Надо найти пересечение множеств.
20+17-32=5 учащихся
Задача 3
Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят лилии, а пятеро – фиалки. И только у двоих есть и лилии и фиалки. Угадайте сколько у меня подруг?
Решение
А - лилии
В - фиалки
Пересечение множеств равно 2 ( и лилии, и фиалки)
6 – 2 = 4 – разводят только лилии
5 – 3 = 2 – разводят только фиалки
4 + 3 + 2 = 9 (подруг)
Задача 4
В классе 40 человек. Из них по математике имеют тройки-17 человек, по русскому языку- 19 человек, по физике 22 человека. 4 человека имеют тройки только по русскому языку , 4 только по математике и 11 человек только по физике. Пять человек имеют тройки по русскому языку, математике и физике. Сколько человек учатся без троек?
А – множество учащихся, имеющих тройки по русскому языку.
В – множество учащихся, имеющих тройки по математике.
С – множество учащихся, имеющих тройки по физике.
Всего в множество В входит 17 человек, значит 17-(4+2+5)=6 (чел. ) – только по русскому и математике.
Всего в множество А входит 19 человек, значит 19-(4+5+6)=4 (чел. ) – только по русскому и физике
Складываем все числа, которые получились на схеме: 4+4+11+6+4+2+5=36.
Всего учащихся 40. Значит без троек учатся 40-36= 4 человека
Задача 5.
В деревне 44 дома, и в каждом доме проживает одна семья. Известно, что 25 семей держат коров , 28 семей – овец и 26 семей – свиней. Причем 15 семей держат коров и овец, 13 семей – овец и свиней, 5 семей – коров, овец и свиней. Сколько семей держат коров и свиней?
А – множество семей, имеющих коров.
В – множество семей, имеющих свиней.
С – множество семей, имеющих овец.
44-[(25-15)+(28-13)+(26-х)]=5
44-25-26+Х
Х=5-44+51
25 – 15 = 10 – семей, имеющих только коров.
28 – 13 = 15 – семей, имеющих только овец.
26 –Х – семей, имеющих только свиней.
Задача 6.
Ученики нашего класса принимали участие в олимпиаде по биологии и русскому языку, часть – только по биологии, а часть в двух олимпиадах. По биологии принимало участие 85%, по русскому языку 75%. Сколько процентов учащихся участвовало в двух олимпиадах?
Решение.
А – множество учеников, принимающих участие в олимпиаде по биологии.
В – множество учеников, принимающих участие в олимпиаде по русскому языку.
100% - все учащиеся.
100% - 85% = 15% Учащиеся, участвующие в олимпиаде только по русскому языку.
75% - 15% = 60% Учащиеся, участвующие в двух олимпиадах.
Задача 7.
В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих, 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и полузащитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Решение.
А – множество нападающих.
В– множество полузащитников.
С – защитники.
30 – [(18 – 3) + (17 – 6) + (11 – 10) + 1] = 30 – 15 – 11 – 1 – 1 = 30 – 28 = 2 (вратаря)
Задача 8.
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение
А – множество человек, которые пользуются метро.
В – множество человек, которые пользуются автобусом.
С – множество человек, которые пользуются троллейбусом.
Пусть Х – пользуются всеми видами транспорта, тогда 20-10=10 – только метро, 23-9=14 – только троллейбусом, 15-12=3 – только автобусом.
Х=30-10-14-3
3 человека пользуются всеми видами транспорта.
Вывод: В результате работы над данной темой мы пришли к следующему выводу: «Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными».
www.hintfox.com
Математическая секция Круги Эйлера
средняя общеобразовательная школа №3 г. Баймака.
Математическая секция
Круги Эйлера.
Выполнила: Ильясова Назгуль,
ученица 5б класса
МОБУ СОШ №3 г. Баймака.
Научный руководитель:
учитель математики
МОБУ СОШ №3 г. Баймака
Мурзабаева Ф.М.
2008
Оглавление.
1. Введение.
а) Исторические сведения.
б) Изображение множества чисел с помощью кругов Эйлера.
2. Решение задач с помощью кругов Эйлера.
а) Простые задачи.
б) Сложные задачи.
3. Заключение.
1. Введение.Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N-множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.
Ну а как же круги Эйлера помогают при решении задач? Для ответа возьмем несколько задач:2. Решение задач с помощью кругов Эйлера.
1. Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
Решение. Составим схему –
В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?Решение. Обратимся к кругам Эйлера:
Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.3. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?Решение.
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.4. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?Решение. 1 способ. Для решения опять воспользуемся кругами Эйлера:
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.2 способ. А можно эту задачу решить задачу другим способом:
20+15+23-10-12-9+х=30, 27+х=30, х=3.5. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?Решение
Ахотя бы 1+ Н = 34
Ф + Н = 25
Н = 6
А + Н = на 3 человека >, чем Ф + Н = х
одновр. одновр.
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Всего 40 человек.4. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и
холодильник и микроволновку, 19 - и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Решение:
Купили только холодильники: 35-(20-3)-(15-3)-3=4.
Купили только микроволновки: 36-(20-3)-(19-3)-3=0.
Купили только телевизоры: 37-(15-3)-(19-3)-3=6.
Тогда всего покупателей было: 4+17+3+16+12+6=58.
65-58=7 посетителей магазина не купили ничего.
Заключение.В результате работы над данной темой я пришел к следующим выводам:
1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
2) Любое натуральное число является элементом любого следующего множества.
3) Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
vcvetu.ru
Тема: Круги Эйлера
Тема:Круги Эйлера.
Выполнила: Нестеренко Марина
ученица 9б класса школы №367
«Школа надомного обучения
Научный руководитель:
учитель математики
Монакова Клара Захаровна
2010 г.
Оглавление.
1. Введение.
а) Исторические сведения.
б) Изображение множества чисел с помощью кругов Эйлера.
2. Решение задач с помощью кругов Эйлера.
а) Простые задачи.
б) Сложные задачи.
3. Заключение.
1. Введение.
Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N-множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество вех действительных чисел.
Ну а как же круги Эйлера помогают при решении задач? Для ответа возьмем несколько задач:
2. Решение задач с помощью кругов Эйлера.
1. Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
Решение. Составим схему –
В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).
2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Решение. Обратимся к кругам Эйлера:
Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
3. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Решение.
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.
4. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Решение. 1 способ. Для решения опять воспользуемся кругами Эйлера:
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом:
20+15+23-10-12-9+х=30, 27+х=30, х=3.
5. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Решение
Ахотя бы 1+ Н = 34
Ф + Н = 25
Н = 6
А + Н = на 3 человека >, чем Ф + Н = х
одновр. одновр.
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 – х – 3 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Всего 40 человек.
4. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и
холодильник и микроволновку, 19 - и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Решение:
Купили только холодильники: 35-(20-3)-(15-3)-3=4.
Купили только микроволновки: 36-(20-3)-(19-3)-3=0.
Купили только телевизоры: 37-(15-3)-(19-3)-3=6.
Тогда всего покупателей было: 4+17+3+16+12+6=58.
65-58=7 посетителей магазина не купили ничего.
Заключение.
В результате работы над данной темой я пришла к следующим выводам:
1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
2) Любое натуральное число является элементом любого следующего множества.
3) Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
dmee.ru
Эйлер и его круги — Iteach
Материал из ИнтеВики — обучающей площадкой для проведения тренингов программы Intel
Пример ученической работы
Вопросы для исследования:
Какие методы решения логических задач оставили ученые своим потомкам?
Какова роль кругов Эйлера в решении задач?
Цель работы: изучить биографию Эйлера, познакомиться с кругами Эйлера, составить и научиться решать задачи, применяя круги Эйлера, развить умения наблюдать и анализировать, выделять существенные признаки и на их основе делать выводы.
Ход исследования:1. Познакомиться с литературой и источниками по данному вопросу.
2. Изобразить множества чисел с помощью кругов Эйлера.
3. Составить и решить задачи с помощью кругов Эйлера.
Диаграммы Эйлера-Венна
Составление и решение задач с помощью кругов Эйлера.
а) Простые задачи.
б) Сложные задачи.
ЛЕОНАРД ЭЙЛЕРЭйлера называют идеальным математиком 18 века. Эйлеру повезло: он родился в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри. Так переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского питомника гениев.
Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику под руководством, первыми образцами которых явились классические монографии Эйлера. Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный. Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами. Используется в математике, логике, менеджменте и других прикладных направлениях. А впервые он их использовал в письмах к немецкой принцессе. Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». Позднее аналогичный прием использовал ученый Венн и его назвали «диаграммы Венна». Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов: N - множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел, R – множество всех действительных чисел.
Решение задач с помощью кругов Эйлера.1. Ученики нашего класса принимали участие в олимпиаде по биологии и русскому языку, часть –только по биологии, а часть в двух олимпиадах. По биологии принимало участие 85%, по русскому языку 75%. Сколько процентов учащихся участвовало в двух олимпиадах?
Решение. Составим схему – Файл:Doc.5/100px/thumb/center В кружке под буквой «Б» обозначим учащихся, участвующих в олимпиаде по биологии, под буквой «Р» - по русскому языку. В общей части кружков обозначим учащихся, участвующих в двух олимпиадах. Теперь от всех учащихся (100%) отнимем кружок «Б» (85%), получим учащихся, участвующих только по русскому языку (15%). А теперь от всех, участвующих по русскому языку (75%), отнимем эти 15%. Получим участвующих в двух олимпиадах (60%). Ответ: 60%.
2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят лилии, а пятеро — фиалки. И только у двоих есть и лилии и фиалки. Угадайте, сколько у меня подруг?
Решение. Файл:Doc.6/100px/thumb/center Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц лилий, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2, так как лилии и фиалки у двоих. В оставшейся части круга «лилий» ставим цифру 4 (6 − 2 = 4). В свободной части круга «фиалок» ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг. Ответ: 9 подруг.
3. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Решение. Файл:Doc.7/100px/thumb/center 18 + 11 + 17 - 3 - 10 - 6 + 1 = 28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит, вратарей будет 30 - 28 = 2. Ответ: 2 вратаря. 4. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение. 1 способ. Для решения опять воспользуемся кругами Эйлера: Файл:Doc.8/100px/thumb/center Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро: 20 − (12 − х) − (10 − х) − х = х − 2 Аналогично получаем: (х − 6) — только автобусом и (х + 4) — только троллейбусом, так как всего 30 человек, составляем уравнение: Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3. Ответ: 3.
2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 - 10 - 12 - 9 + х = 30, 27 + х = 30, х = 3. 5. В восьмом классе учится 40 человек. Каждый из них изучают не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
Решение А + Н = 34 Ф + Н = 25 Н = 6 А + Н = на 3 человека >, чем Ф + Н = х одновременно Файл:Doc.9/100px/thumb/center 34 – х – 3 – 6 – х + х + 3 + 6 + х + 25 – х – 6 – х – 3 = 40 – 2х = 40 – 34 + 3 – 25 – 2х = –10 х = 5 Ф + Н = 5 человек. А + Н = 8 человек. А = 34 – 8 – 6 – 5 =15 человек. Н = 6 человек. Ф = 25 – 5 – 6 –8 = 6 человек. Всего 40 человек.
4. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 магнитофонов, 37 телевизоров. 20 из них купили и холодильник и магнитофон, 19 - и магнитофон, и телевизор, 15 - холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Решение: Файл:Doc.10/100px/thumb/center Купили только холодильники: 35 - (20 - 3) - (15 - 3) - 3 = 4. Купили только магнитофоны: 36 - (20 - 3) - (19 - 3) - 3 = 0. Купили только телевизоры: 37 - (15 - 3) - (19 - 3) - 3 = 6. Тогда всего покупателей было: 4 + 17 + 3 + 16 + 12 + 6 = 58. 65 - 58 = 7 посетителей магазина не купили ничего. Ответ: 7.
5. Спортивный класс
Файл:Doc.11/100px/thumb/centerВ классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекается одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?
Решение. Файл:Doc.12/100px/thumb/center Воспользуемся кругами Эйлера. Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта - баскетболом занимаются 16 - (4 + z + 3) = 9 - z; одним лишь хоккеем 17 - (4 + z + 5) = 8 - z; одним лишь футболом 18 - (3 + z + 5) = 10 - z. Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочками: 3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38, z = 2. Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек. Ответ: Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.
ВыводыВ результате работы над данной темой мы пришли к следующим выводам: 1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью; 2) Любое натуральное число является элементом любого следующего множества. 3) Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
Учебный проект Логика в математике
wiki.iteach.ru
Проектная презентация "Круги Элера" - математика, презентации
Проект:
Круги Эйлера
Руководитель проекта: Маданова Елена Анатольевна
- Авторы проекта: Клычникова Саша
Козлова Марина
Ботов Илья
Мисерова Юля
Кузмичёва Юля
Брик Артём
Такташев Дима
Гришин Антон
- Применение кругов Эйлера придаёт задачам наглядность и простоту.
Мы знаем об этом мало.
ЦЕЛЬ:
- Изучить и показать, как изображение
условий задачи в виде кругов Эйлера
упрощают и облегчают путь к её решению.
- 1.Собрать материал о кругах Эйлера, рассмотреть их по принципу «от простого к сложному». Показать, как в задачах вводится символика алгебры множеств.
- 2.Представить информацию в виде компьюторной презентации.
- 3.Прорешать задачи за «круглым столом».
- 4.Оформить буклеты с задачами, для ознакомления другими ребятами.
Леонард Эйлер ( 1707 - 1783 ).
Повезло Эйлеру : он родился в маленькой тихой Швейцарии. Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику под руководством, первыми образцам которых явились классические монографии Эйлера. Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный. Его называли идеальным математиком 18 века. Леонард Эйлер написал более 850 научных работ. В одной из них и появились круги. При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов . Этот метод даёт более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.
Задачи по принципу « от простого к сложному»
1. Часть жителей Башкирии говорят только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
- Решение. Составим схему –
В кружке под буквой «Б» обозначим жителей, говорящих по-башкирски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «Б» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).
2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
- Решение. Составим схему –
Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
3. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
- Решение. Обратимся к кругам Эйлера:
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит, вратарей будет 30-28=2. Ответ: 2 вратаря.
4. В классе 30 человек. 20 из них каждый день пользуются метро, 15 — автобусом, 23 — троллейбусом, 10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
- Решение. 1 способ. Для решения воспользуемся кругами Эйлера:
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом:
20+15+23-10-12-9+х=30, 27+х=30, х=3.
, чем Ф + Н = х одновр. одновр. 34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 = 40 – 2х = 40 – 34 + 3 – 25 – 2х = –10 х = 5 Ф + Н = 5 человек. А + Н = 8 человек. А = 34 – 8 – 6 – 5 =15 человек. Н = 6 человек. Ф =25 – 5 – 6 –8 = 6 человек. Всего 40 человек."
5. В восьмом классе учится 40 человек. Каждый из них изучает не менее одного иностранного языка: английский, немецкий, французский. 34 человека изучают хотя бы один из двух языков: английский, немецкий. 25 человек — хотя бы один из языков: немецкий, французский. 6 человек только немецкий. Одновременно два языка — английский и немецкий — изучают на 3 человека больше, чем французский и немецкий языки. Сколько человек изучает каждый из языков и сколько изучает одновременно каждую пару языков?
А + Н = 34
Ф + Н = 25
Н = 6
А + Н = на 3 человека , чем Ф + Н = х
одновр. одновр.
34 – х – 3 – 6 – х + х + 3 + 6 + х +25 – х – 6 = 40
– 2х = 40 – 34 + 3 – 25
– 2х = –10
х = 5
Ф + Н = 5 человек.
А + Н = 8 человек.
А = 34 – 8 – 6 – 5 =15 человек.
Н = 6 человек.
Ф =25 – 5 – 6 –8 = 6 человек.
Всего 40 человек.
В результате работы над данной темой мы пришли к следующим выводам :
- 1) Все множества чисел связаны между собой так, что каждое следующее, более объемное, включает в себя предыдущее множество полностью;
- 2) Любое натуральное число является элементом любого следующего множества.
- 3) Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
kopilkaurokov.ru
