pdf математика / Теория вероятностей в примерах и задачах. Что неправильно в сообщении спартак выиграет с вероятностью 200
8 основ успешного беттинга. Насколько важна теория вероятностей? - Serenity Bets - Блоги
Продолжаем серию полезных статей по ставкам. Предыдущие 4 поста можно почитать, кликнув на гиперссылки ниже:
На сей раз речь пойдёт об основах ставок, не зная которых, невозможно преуспеть в этой деятельности. А именно о том, почему нужно учитывать теорию вероятностей и ориентироваться на дистанционную прибыль. Так или иначе, я уже касался этой темы множество раз, но данный пост раскроет её в полной мере.
Где-то в марте наткнулся на одну интересную статью, которую возьму за базу (не буду приводить источник, дабы не рекламировать сайт, однако погуглив, уверен, вы найдёте растиражированный подробный оригинал). Впервые в блоге будет представлен материал, который не написан мной лично "от корки до корки". Немного отредактировав статью, убрав «воду» и сократив для более удобного восприятия, добавив картинок и своих мыслей, представляю публике, т.к. считаю, что это действительно важная вещь, и она не должна быть обойдена стороной.
Итак, 8 принципов, отталкиваясь от которых, можно поменять свой подход к ставкам и начать на них зарабатывать.
№1 Большинство азартных игроков считает, что теория вероятностей в ставках на спорт не работает, т.к. на результат спортивного матча влияет слишком много случайностей, в том числе очень многое зависит от человеческого фактора. Был приведён хороший пример, что это то же самое, будто считать, что земное притяжение не действует на самолёт, раз оно позволяет ему летать, несмотря на массу в несколько сотен тонн. То, что результат спортивного матча зависит от множества случайностей, говорит лишь о том, что мы не можем заранее и точно знать вероятность этого результата. Однако это не мешает работать законам математики и теории вероятностей, существующим независимо от конкретных событий, аксиоматично, и по сути, являющимся основой ставочной деятельности.
№2 Важный аспект с монеткой, который я привожу почти каждый раз, когда ведётся спор на тему дистанционной прибыли. Превосходная аналогия. Вероятность выпадения одной из сторон идеальной монетки 50% = 0.5 или 1/2, означает, что в среднем каждая из сторон должна выпадать один раз из двух бросков. Но на деле вы можете бросить монетку десять раз, и все десять - выпадет, например, решка. Этот нюанс называется дисперсией, и именно он часто вводит в заблуждение многих игроков. На самом деле величина вероятности означает частоту, с которой это событие будет встречаться при бесконечном количестве попыток. Чем меньше испытаний, тем больше (в процентном отношении) реальный результат может отклоняться от математического ожидания. Это и есть дисперсия.
№3 ЖБ, "100% верняков" или беспроигрышных ставок не существует. Реальную вероятность спортивного события не знает никто, даже букмекер. Упрощённо можно сказать, что эту самую вероятность он оценивает, выдавая коэффициент на данное событие. И эта оценка примерно равна величине 1/коэффициент. Коэффициент 1.10 примерно отражает вероятность 1/1.10 = 90.9%. Что можно на словах описать, как событие, которое должно происходить в среднем 9 раз из 10. Однако нельзя забывать про дисперсию. На короткой дистанции событие с указанной вероятностью может случиться и 20 раз из 20 (что часто вводит в эйфорию неопытных игроков, поймавших подобную удачную серию, которая заставляет их поверить в то, что они – эксперты, и сейчас-то они просто разорвут букмекеров). А может не произойти два, три и даже четыре раза подряд, хотя последнее будет случаться довольно редко, но всё же будет, время от времени.
Если считать, что коэффициент букмекера примерно соответствует реальной вероятности события (что по совокупности нескольких ставок будет недалеко от истины), то вероятность неудачной серии из N проигранных ставок подряд можно вычислить по формуле: (1 - 1/коэффициент) в степени N. Для четырех проигрышей подряд коэффициента 1.10 получаем вероятность (1 - 1/1.10) в степени 4 = 0,0000683 или, округлённо, 1 раз из 14 000. Однако помним про дисперсию, да? Это вовсе не значит, что вы можете безопасно "проскочить" 13 999 раз, и "попасть" ровно на 14 000-й. Нет, с абсолютно одинаковыми шансами такое несчастье может случиться с вами как существенно позже 14 000-го раза, так и сразу - с первой попытки, а также и более одного раза на каком-то из отрезков в 14 000 испытаний.
И оно не зависит от того, насколько вы уверены в данной ставке. Ещё одно распространённое заблуждение заключается в том, что многие игроки считают: после проигрыша одной, а тем более нескольких ставок подряд,вероятность выигрыша следующей ставки увеличивается. И поэтому используют прогрессивные стратегии ставок, такие, как догон (читаем статью про догон---> здесь <---).
Увы, всё совсем не так, это психологическая ловушка. На деле вероятность выигрыша вашей ставки никак не зависит от того, сколько раз вы проиграли перед этим. То же самое после того, как вы выбросили несколько "орлов" подряд, вероятность выкинуть в следующем броске "решку" у идеальной монетки не меняется и остаётся те же 50%.
(!) Именно поэтому ни в коем случае не лезьте отыгрываться. Умейте вовремя остановиться. Все эти истории, когда человек считает, что ему не может столько не везти, ставит ещё и ещё, увеличивает ставку в надежде перекрыть всё проигранное, до добра не доводят, - можно вообще остаться банкротом. Если кто следит за ставочным разделом, помнят историю проигравшегося лудомана, опубликованную в "Форе ноль" (фейк именно это или нет - другой вопрос, но что подобные существуют реально - это факт).
№4 Нельзя делать уверенные выводы о том, прибыльны ли на дистанции ставки или нет, после всего лишь условных 10 попыток. Из-за дисперсии ваш реальный результат на дистанции может очень сильно отличаться от показанного на коротком отрезке. Чем выше коэффициент - тем выше дисперсия, тем больше нужно сделать ставок, чтобы понять, куда они вас заведут.
Вы должны оценивать прибыльность или убыточность своих ставок именно на дистанции, если вы всерьёз и надолго собираетесь зарабатывать, делая ставки на спорт, а не рассчитываете поймать удачную полосу ("положительный выброс дисперсии"), забрать деньги и больше никогда не возвращаться к ставкам в букмекерских конторах.
____________________
Здесь же стоит отметить, что не стоит судить не только о своих способностях, но и об успешности любого прогнозиста на основании короткого промежутка времени, на котором он работает.
С одной стороны, если он выдал серию лузов, - не стоит хаять его и говорить, что он – неудачник, не разбирается в спорте и пусть вообще прекращает этот ужас. «Луз-стрики» случаются абсолютно у всех, и каждый, кто заявляет обратное, - лжец. Вопрос лишь в их длительности. И важно, чтобы эти периоды перекрывались успешными.
С другой, не стоит переоценивать и сверхудачные периоды. Многие разводилы пользуются этой схемой.Создают аккаунт, выдают хорошую серию на короткой дистанции (10+ в ряд, например), заманивают себе наивную клиентуру, и далее закрывают бесплатную лавочку, говоря, что так будет и дальше – 100% проходимость, жб-верняк, «атвичаю». Однако потом случаются провалы, о которых широкая общественность уже не узнает. Создаётся новый аккаунт и т.д. Далеко ходить не стоит, даже на sports можно привести несколько свежих примеров (про vk я не говорю). Дабы не делать антипиар, приводить их не буду.
№5 Многие сравнивают букмекерскую деятельность с казино. И там, и там азарт. И там, и там, многие считают, что невозможно выиграть. Однако есть одно существенное отличие букмекерской конторы от казино, которое коренным образом меняет дело. Если в играх казино все вероятности заранее известны, то о вероятностях реальных спортивных событий достоверно неизвестно никому, в том числе и букмекерам. Поэтому вполне реальны, более того, регулярно случаются ситуации, когда букмекеры дают коэффициенты выше 2 на события, чья реальная вероятность оказывается в районе 50%. Что означает прибыль на дистанции для игрока, делающего такие ставки (или value bet, о которых я не раз говорил, именно «вэлью-беттинг» даёт дистанционную прибыль). Косвенные доказательства того, что букмекерские аналитики вовсе не безгрешны при оценке вероятностей событий и выставлении на них коэффициентов, это движения линии, когда, порою, фаворит в матче с течением времени меняется на прямо противоположного.
№6 Секрет успеха в ставках на спорт не противоречит математике или теории вероятностей и на первый взглядформулируется довольно просто: нужно выбирать ставки, в которых коэффициент букмекера неверно оценивает вероятность события, делая его прибыльным для игрока. Соответственно, находя такие события и проставляя их на постоянной основе, и можно иметь заработок.
№7 Чтобы научиться зарабатывать ставками на спорт в букмекерских конторах, крайне важно изменить свои принципы мышления в сторону value-беттинга. Большинство игроков, думая о том, какую ставку сделать, мыслят примерно таким образом: "Я уверен, что Спартак победит Амкар, поэтому поставлю на него". Как вы должны уже понимать, ваша личная уверенность в победе Спартака не даёт никакой практической выгоды, когда речь идёт о правильном выборе ставки на этот матч. Вместо этого вы должны научиться оценивать, как часто Спартак (или любая другая команда) здесь будет побеждать при прочих равных условиях. Например: "Я думаю, что Спартак обыграет Амкар в 8 матчах из 10 при нынешнем состоянии этих команд".
Далее вы смотрите коэффициент букмекера на данное событие. Предполагаемая вами частота побед Спартака 8 из 10 (или оценка вероятности 8/10 = 0.8) соответствует безубыточному коэффициенту 1.25 (1 / 0.8). То есть, если букмекер даёт 1.30, то это будет выгодная ставка на дистанции. Однако если бы вы предположили, что Спартак будет побеждать Амкар в 7 случаях из 10, то коэффициент безубыточности должен быть уже 1.43. Казалось бы, разница всего в одну победу, а коэффициенты по выплате (то есть по чистой полученной вами прибыли без учета суммы ставки) отличаются почти в два раза! Вот как велико влияние вроде бы самой минимальной погрешности вашей оценки на низких коэффициентах. А ведь, возможно, и 7 из 10 в реальности будет слишком оптимистичной оценкой.
Именно поэтому любители ставок типа «РЕАЛ ПЭ ОДИН!!!» в любой ситуации за крошечные коэффициенты, ставших уже своего рода мемом, весьма часто остаются с носом в итоге.
№8 Если резюмировать, вы должны очень хорошо разбираться одновременно и в математике, и в статистике, и в теории вероятностей, и в принципах выставления букмекерских коэффициентов, и в том виде спорта, на который хотите делать ставки, чтобы успешно определять события, в которых букмекер необоснованно завысил коэффициент, и этого завышения достаточно для того, чтобы, делая ставки на такие события, иметь прибыль на дистанции. Всё приходит с опытом, если есть интеллектуальный потенциал.
Надеюсь, материал оказался для Вас полезным. Если так, ставим 
и подписыаемся:) Не гонитесь за сиюминутной наживой и смотрите чуть дальше своего носа. Используем принципы, описанные выше, читаем аналитику от Serenity Bets, включаем голову, и получаем дистанционный доход.
__________________________________________
P.S. Ознакомиться с итогами и планами группы/блога можно здесь:
Что день грядущий уготовил нам? Итоги и планы Serenity Bets
Ещё больше ставок, обсуждений и полезной информации в группе вконтакте. Подписывайтесь и держите руку на пульсе, получайте прогнозы первыми (кликаем ссылку или картинку ниже) --->> Serenity Bets <<---
www.sports.ru
Теория вероятностей в примерах и задачах
96. Пусть событияA, B иC попарно независимы, причём каждое из них име- ет вероятность, отличную от нуля и единицы. Проверить, могут ли событияA ∩B , B ∩C иA ∩C быть: а) попарно независимыми; б) независимыми в совокупности.
РЕШЕНИЕ. а) Рассмотрим следующие события в условиях задачи47: событиеA , заключающееся в том, что утечка газа происходит ближе к станцииA, чем кB, событиеB , заключающееся в том, что утечка расположена между50-ми150-мкилометрами, и событиеC , состоящее в том, что утечка расположена между отметками12,5 км и62,5 км либо между112,5 км и162,5 км. Тогда, со-
гласно геометрическому определению вероятности, P{A}= P{B}= P{C}= 21 , P{A∩B}= P{B ∩C}=
=P{A∩C}= 41 , значит, событияA,B иC попарно независимы. При этом, очевидно, P{A∩B∩C}=
= 161 ,P{(A ∩B)∩(B ∩C )} =P{A ∩B ∩C} =161 =P{A}[P{B}]2 P{C} =P{A ∩B}P{B ∩C} .Аналогич-
но получаем равенства P{(A∩B) ∩(A∩C )}= P{A∩B}P{A∩C} иP{B∩C ) ∩(A∩C )} = P{B∩C}P{A∩C} ,
т. е. событияA , B иC являются независимыми в совокупности. б) Независимость в совокупно- сти означает, во-первых, чтоP{A ∩B ∩C} = P{(A ∩B)∩(B ∩C)} = P{A}[P{B}]2 P{C} и, во-вторых,
что P{A∩B∩C}=P{(A∩B)∩(B∩C )∩(A∩C)}=[P{A}]2[P{B}]2[P{C}]2 .Поэтому P{A}[P{B}]2 P{C}= =[P{A}]2[P{B}]2[P{C}]2 ,но это равенство невозможно,так как вероятности событий A ,B и C от-
личны от нуля и единицы. Поэтому событияA ∩B , B ∩C иA ∩C не могут быть независимыми в совокупности.
97.Пусть события A, B иC независимы в совокупности, причём каждое из
них имеет вероятность, отличную от нуля и единицы. Проверить, могут ли собы- тияA ∩B , B ∩C иA ∩C быть: а) попарно независимыми; б) независимыми в со- вокупности.
98.Подбрасываются три игральные кости. СобытиеA состоит в том, что на первой и второй костях выпало одинаковое число очков, событиеB — в том, что на второй и третьей костях выпало одинаковое число очков, событиеC — в том, что на первой и третьей костях выпало одинаковое число очков. Проверить, явля- ются ли событияA, B иC : а) попарно независимыми; б) независимыми в сово- купности.
99.Привести пример попарно независимых событий, не являющихся при этом независимыми в совокупности.
100.Доказать, что из равенстваP{A ∩B ∩C} = P{A}P{B}P{C} не следует по-
парная независимость событий A, B иC .
101.Доказать формулу (2.7).
102.Пусть A, B — произвольные события. Проверить, образуют ли событияA,
A ∩B , A B полную группу.
103.Доказать формулу полной вероятности (2.8).
104.Доказать формулу Байеса (2.9).
105.Статистика запросов кредитов в банке такова: 10% — государственные ор- ганы, 20% — другие банки, остальные— физические лица. Вероятности того, что взятый кредит не будет возвращён, составляют0,01, 0,05 и0,2 соответственно. Оп- ределить, какая доля кредитов в среднем не возвращается.
РЕШЕНИЕ. Пусть событиеA состоит в том, что взятый кредит не возвращается, гипотезаh2 — в том, что запрос на этот кредит поступил от государственного органа, гипотезаh3 — в том, что запрос на кредит поступил от другого банка, гипотезаh4 — в том, что запрос на кредит посту-
studfiles.net
§4. Формулы Бернулли, Лапласа и Пуассона
Формула Бернулли. Вероятность того, что вnнезависимых испытаниях, в каждом из которых вероятность появления события равна р (0<p<1), событие наступит равноkраз (безразлично в какой последовательности), равна
где .
При больших nэта вероятность может быть приближенно вычислена по формуле Лапласа:
где .
Значения функции φ(x) для положительных х затабулированы, а для отрицательных х следует воспользоваться четностью функции: φ(-x)= φ(x).
Если nвелико, а вероятность появления события близка к нулю, то большую точность вычисления дает приближенная формула Пуассона:
где .
Интегральная теорема Лапласа. Вероятность того, что вnнезависимых испытаниях, в каждом из которых вероятность появления события равнаp(0<p<1), событие наступит не менееk1раз и не болееk2раз, приближенно равна
где
Интегральная функция Лапласа Ф(x) затабулирована дляx>0, приx<0 следует использовать свойство нечетности функции Ф(-x)=Ф(x).
Пример 48.В каждом из 700 независимых испытаний событие А происходит с постоянной вероятностью 0.35. Найти вероятность того, что событие А произойдет: а) 270 раз; б) не менее 230 и не более 270 раз; в) не менее 270 раз.
Решение.По условию задачиn=700;p=0.35;q=0.65. Посколькуnдостаточно велико, воспользуемся приближенными формулами Лапласа.
а) k=270. НайтиP700(270).
По таблице находим:
.
б) k1=230,k2=270. НайтиP700(230≤k≤270).
.
Значения Ф(x) найдем по таблице:
в) k≥270. НайтиP700(270≤k≤700).
.
Пример 49. Вероятность поражения мишени при одном выстреле равна 0.4. Найти вероятность того, что при 4 выстрелах мишень будет поражена: а) 3 раза; б) не менее 3 раз; в) хотя бы один раз.
Решение.По условиюn=4;p=0.4;q=0.6.
а)
б) .
в) .
Пример 50. На телефонной станции неправильное соединение происходит с вероятностью 0,005. Найти вероятность того, что среди 200 соединений произойдет: а) одно неправильное соединение; б) меньше 3 неправильных соединений; в) больше 2 неправильных соединений.
Решение. Вероятность рассматриваемого события мала, поэтому воспользуемся формулой Пуассона. По условию n=200, λ=np=200*0.05.
а) k=1, Найти: P200(1).
По формуле Пуассона:
б) k<3. Найти: P200 (0≤k<3).
P200 (0≤k<3)=P200 (0)+ P200(1)+ P200 (2)=e-1 (1+1+0,5)=0,9197.
в) k>2. Найти: P200(k>2).
Эту задачу проще решить, если перейти к противоположным событиям.
P200(k>2)=1- P200(k≤2)=1-( P200(0)+ P200(1)+ P200(2))=
=1-P200(k<3)=1-0,9197=0,0803.
51. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.
52. Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t если:
а) работают только основные элементы;
б) включен один резервный элемент;
в) включены два резервных элемента.
Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента также равна 0,1 и устройство отказывает, если работает менее трех элементов.
53. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
54. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
55. Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится: а) не менее 1470 и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.
56. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?
57. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных.
58. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) менее двух; в) более двух; г) хотя бы одну.
59. Изготовитель радиоэлектронного оборудования закупает 1000 интегральных микросхем, каждая из которых с вероятностью 0,01 может оказаться неисправной. Какова вероятность того, что
а) неисправны будут ровно 10 микросхем?
б) все микросхемы окажутся исправными?
в) из всех микросхем неисправна будет лишь одна?
studfiles.net
2. Примеры решения задач
P(A) =P(A|h2)·P(h2) +P(A|h3)·P(h3) +P(A|h4)·P(h4) = = 0,9×0,25 + 0,85×0,5 + 0,8×0,25 = 0,85.
Вероятность того, что правильный счет обнаружен у первой фирмы
P(h2|A) =P(A|h2)·P(h2)/P(A) = 0,9×0,25/0,85 = 0,26.
Вероятность того, что правильный счет обнаружен у второй фирмы
P(h3|A) =P(A|h3)·P(h3)/P(A) = 0,85×0,5/0,85 = 0,5.
Ответ: среди правильных счетов больше счетов второй фирмы.
6. Формула Бернулли
Вероятность продажи акций с прибылью через год после покупки равна 0,8. Независимо было продано 5 акций. Найти вероятность того, что прибыль будет получена ровно с двух из них.
Решение
Обозначим p = 0,8 – вероятность выгодной продажи одной акции,q =
1 – p = 0,2 – вероятность невыгодной продажи одной акции через год после покупки. Тогда вероятность выгодной продажи ровно двух акций
P (2 )= C2 p2q5-2 | = | 5! | 0,820,23 = 0,0512. | |
| ||||
5 | 5 | 2!×3! | ||
|
| |||
Ответ: 0,0512
7. Приближения в схеме Бернулли
a. Вероятность того, что учебник неправильно переплетен, равна 0,002. В библиотеку поступило 500 учебников. Какова вероятность того, что среди поступивших учебников более 2 неправильно переплетенных.
Решение
Использовать формулу Бернулли невозможно из-забольшого количества испытаний. Поскольку количество испытаний велико(500 учебников > 50), а успех редкий (0,002 < 0,1), можно использовать формулу Пуассона для оценки вероятности события.
Обозначим событие «среди поступивших учебников более 2 неправильно
переплетенных» как A. Тогда | событие, противоположное A (`A) – «среди | |||||||
поступивших учебников не более2 неправильно переплетенных», является | ||||||||
суммой | событий B0 | «среди | поступивших | учебников | нет | неправильно | ||
переплетенных», | B1 | «среди | поступивших | учебников одиннеправильно | ||||
переплетенный» | и | B2 | «среди | поступивших | учебников | два | неправильно | |
studfiles.net
Теория вероятности_Белов_вар 20
РАЗДЕЛ I
20. Из полной колоды карт (52 листа) извлекают сразу несколько карт. Сколько карт нужно извлечь для того, чтобы с вероятностью, большей чем 0,5, утверждать, что среди них будут содержаться карты одной и той же масти?
Решение.
Воспользуемся классической формулой вероятности
,
где m– число благоприятных исходов,
n– число всех исходов.
Обозначим искомое число через k. Прежде всего заметим, что если k > 4 , то среди выбранных карт наверняка найдутся карты одной и той же масти. Значит, нужно рассмотреть случаи, когда k = 2, 3, 4.
1. k = 2, число элементарных исходов равно .
Событие A = {две карты одной масти} есть сумма четырех несовместных событий: A = А1 + А2 + A3 + А4, где событию Ai (i = 1, 2, 3, 4) соответствует фиксированная масть. Так как (Выбираются любые две карты из 13 карт данной масти), то.
Тогда p(A) = 312/1326 = 0,235 < 0,5.
2. k = 3, . Найдем число исходов, входящих в событие.
Чтобы выбрать три карты разных мастей, нужно сначала выбрать три определенные масти из четырех. А затем выбрать по одной карте из тринадцати карт каждой из выбранных мастей.
Значит, .
Тогда , а вероятность события A = {есть карты одной масти} равна: p(A) = 13312/22100 = 0,602 > 0,5.
Ответ: нужно выбрать не меньше трех карт.
РАЗДЕЛ II
Игра проводится до выигрыша одним из двух игроков 2 партий подряд (ничью исключаются). Вероятность выигрыша партии каждым из игроков равна 0,5 и не зависит от исходов предыдущих партий. Найдите вероятность того, что игра окончится до 6 партии.
Решение.
p = 0,5 – вероятность выигрыша одним игроком
А - игра окончится до 6 партии
Ответ: вероятность того, что игра окончится до 6 партии, равна 0,406.
РАЗДЕЛ III
2. Имеются 2 урны. В первой 3 белых и 4 черных шара, во второй – 2 белых и 3 черных шара. Из первой урны наудачу перекладывают во вторую 2 шара, а затем из второй урны извлекают один шар. Он оказался белым. Какова вероятность того, что в первой урне осталось 2 белых и 3 черных шара?
Решение.
Воспользуемся формулой Байеса:
Существует 3 гипотезы:
В1– из первой урны переложили два белых шара,
В2– из первой урны переложили один белый и один черный шар,
В3– из первой урны переложили два черных шара,
Найдем вероятности гипотез:
; ;
Найдем условные вероятности (шар, вынутый из 2-й урны, оказался белым): ;;
Чтобы в первой урне осталось 2 белых и 3 черных шара, из нее необходимо вытащить 1 белый и 1 черный шар (вторая гипотеза В2):
Ответ:вероятность того, что в первой урне осталось 2 белых и 3 черных шара, равна 0,6.
РАЗДЕЛ IV
3. Производится 4 независимых опыта, в каждом из которых событие А происходит с вероятностью 0,3. Событие В наступает с вероятностью 1, если событие А произошло не менее двух раз; не может наступить, если событие А не имело места, и наступает с вероятностью 0,6, если событие А имело место один раз. Найдите вероятность события В.
Решение.
Воспользуемся формулой полной вероятности:
А – выбранный стрелок попадет в цель.
Найдем вероятности гипотез:
В1– событие А не имело места,
В2– событие А произошло один раз,
В3– событие А произошло два раза,
В4– событие А произошло три раза,
В5– событие А произошло четыре раза.
Р(В1) =
Р(В2) =
Р(В3) =
Р(В4) =
Р(В5) =
Проверка: Верно.
Найдем условные вероятности:
Вероятность того, что событие В наступит
Ответ: вероятность того, что событие В наступит, равна 0,59526.
РАЗДЕЛ V
4. Существуют ли предельные вероятности для цепи Маркова, управляемой матрицей перехода, (если да, то найдите их):
Решение.
Все вероятности лежат в интервале 0 ≤ рij≤ 1
∑р1j= 0,5 + 0,5 = 1;
∑р2j= 0,3 + 0,7 = 1
Следовательно, к данной цепи применима теорема Маркова.
Так как матрица А не равна матрице А2, то предельные вероятности существуют.
Найдем предельные вероятности:
;;;
Проверка: Верно.
Ответ: предельные вероятности существуют и равны р1= 0,375,p2= 0,625.
РАЗДЕЛ VI
5. По мишени ведутся выстрелы до первого попадания или до израсходования всех имеющихся патронов. Построить таблицу распределения, многоугольник распределения и функцию распределения случайной величины Х – числа израсходованных патронов, если вероятность попадания при отдельном выстреле равна р = 0,3, а патронов всего 4.
Решение.
Возможные значения случайной величины Х: 1, 2, 3, 4.
р = 0,3 – вероятность попадания в мишень.
n =4 – количество патронов.
Тогда ряд распределения величины Х имеет вид:
| Х | 1 | 2 | 3 | 4 |
| Р | 0,3 | 0,21 | 0,147 | 0,343 |
Проверим условие нормировки:
Верно.
Построим многоугольник распределения случайной величины X.
Рис. 1. Многоугольник распределения СВ Х
Составим функцию распределения:
.
Функция распределения имеет вид:
F(X)
X
Рис. 2. Функци яраспределения СВ Х
РАЗДЕЛ VII
6. Плотность вероятности случайной величины Х имеет вид
Найти математическое ожидание и дисперсию случайной величины Х.
Решение.
Математическое ожидание равно:
Дисперсия равна:
Ответ: математическое ожидание равно , а дисперсия равна.
РАЗДЕЛ VIII
Получены следующие опытные данные. Распределение 1000 волокон хлопка по длине:
| Длина волокон, мм. | Число волокон | Длина волокон, мм. | Число волокон |
| 4,5 – 7,5 | 2 | 22,5 – 25,5 | 140 |
| 7,5 – 10,5 | 28 | 25,5 – 28,5 | 170 |
| 10,5 – 13,5 | 51 | 28,5 – 31,5 | 136 |
| 13,5 – 16,5 | 66 | 31,5 – 34,5 | 100 |
| 16,5 – 19,5 | 86 | 34,5 – 37,5 | 72 |
| 19,5 – 22,5 | 128 | 37,5 – 40,5 | 21 |
а) установить гипотетический закон распределения случайной величины;
б) найти его параметры;
в) вычислить гипотетические частоты;
г) пользуясь критерием согласия , установить, согласуются ли опытные данные с предположением о распределении случайной величины по избранному гипотетическому закону.
Уровень значимости принять равным *) 0,05 и **) 0,005.
Решение.
а) установить гипотетический закон распределения случайной величины;
Гипотетически установим в качестве закона распределения СВ Х – нормальный закон распределения.
б) найти его параметры;
Вычислим математическое ожидание:
а ≈ M(x) = 24,843 мм.
Вычислим генеральную дисперсию:
Вычислим среднее квадратичное отклонение:
в) вычислить гипотетические частоты;
Занесем расчеты в таблицу.
| Величина интервала | Количество волокон ni | |||
| xi | xi+1 | |||
| 4,5 | 7,5 | 2 | -2,80 | -2,39 |
| 7,5 | 10,5 | 28 | -2,39 | -1,97 |
| 10,5 | 13,5 | 51 | -1,97 | -1,56 |
| 13,5 | 16,5 | 66 | -1,56 | -1,15 |
| 16,5 | 19,5 | 86 | -1,15 | -0,74 |
| 19,5 | 22,5 | 128 | -0,74 | -0,32 |
| 22,5 | 25,5 | 140 | -0,32 | 0,09 |
| 25,5 | 28,5 | 170 | 0,09 | 0,50 |
| 28,5 | 31,5 | 136 | 0,50 | 0,92 |
| 31,5 | 34,5 | 100 | 0,92 | 1,33 |
| 34,5 | 37,5 | 72 | 1,33 | 1,74 |
| 37,5 | 40,5 | 21 | 1,74 | 2,15 |
| npi | |||
| -0,4974 | -0,49155 | 0,00585 | 5,85 |
| -0,49155 | -0,4756 | 0,01595 | 15,95 |
| -0,4756 | -0,4406 | 0,035 | 35 |
| -0,4406 | -0,3749 | 0,0657 | 65,7 |
| -0,3749 | -0,2703 | 0,1046 | 104,6 |
| -0,2703 | -0,1255 | 0,1448 | 144,8 |
| -0,1255 | 0,0359 | 0,1614 | 161,4 |
| 0,0359 | 0,1915 | 0,1556 | 155,6 |
| 0,1915 | 0,3212 | 0,1297 | 129,7 |
| 0,3212 | 0,4082 | 0,087 | 87 |
| 0,4082 | 0,4591 | 0,0509 | 50,9 |
| 0,4591 | 0,4842 | 0,0251 | 25,1 |
г) пользуясь критерием согласия , установить, согласуются ли опытные данные с предположением о распределении случайной величины по избранному гипотетическому закону. Уровень значимости принять равным 0,05 и 0,005.
| i | ni | ni*=npi | ni- npi | ||
| 1 | 30 | 21,80 | 8,2 | 67,24 | 3,084404 |
| 2 | 51 | 35 | 16 | 256 | 7,314286 |
| 3 | 66 | 65,7 | 0,3 | 0,09 | 0,00137 |
| 4 | 86 | 104,6 | -18,6 | 345,96 | 3,307457 |
| 5 | 128 | 144,8 | -16,8 | 282,24 | 1,949171 |
| 6 | 140 | 161,4 | -21,4 | 457,96 | 2,837423 |
| 7 | 170 | 155,6 | 14,4 | 207,36 | 1,332648 |
| 8 | 136 | 129,7 | 6,3 | 39,69 | 0,306014 |
| 9 | 100 | 87 | 13 | 169 | 1,942529 |
| 10 | 72 | 50,9 | 21,1 | 445,21 | 8,746758 |
| 11 | 21 | 25,1 | -4,1 | 16,81 | 0,669721 |
| å | 31,49 | ||||
χ2набл= 31,49
k=s– 1 – 1 = 9 – число степеней свободы
χ2кр(0,05; 9) = 16,9
χ2кр(0,005; 9) = 23,2
Так как χ2кр< χ2наблпри обоих уровнях значимости, то гипотезу о распределении СВ Х по нормальному закону отвергаем при уровнях значимости α = 0,05 и α = 0,005.
Ответ: следовательно, распределение волокон хлопка по длине не подчинено нормальному закону при уровнях значимости α = 0,05 и α = 0,005.
Список используемой литературы
Гмурман В.Е. Теория вероятностей и математическая статистика. - Изд.4-е, доп. – М.: Высшая школа, 1972.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие. – 11-е изд., перераб. – М.: Высшее образование, 2006.
16
studfiles.net
Формула полной вероятности, формула Байеса.
Задача № 6
Имеются 4 урны с шарами. В первых трех по 1 белому и 1 черному, в четвертой - 4 белых и 1 черный.
1. Из наугад взятой урны достали шар. Найти вероятность того, что он белый.
2. Наугад вынутый шар оказался белым. Найти вероятность того, что он из четвертой урны.
Решение.
1. Пусть событие А состоит в том, что вынутый шар – белый. Это событие наступает в результате появления одного из двух несовместных событий (гипотез): В1 – выбрали одну из первых трех урн;
В2 – выбрали четвертую урну.
Очевидно, вероятности гипотез равны Р(В1)=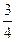 
, Р(В2)= 
.
Тогда, по формуле полной вероятности
.
Здесь 
- вероятность извлечь белый шар из урны с одним белым, одним черным шарами, 
- вероятность извлечь белый шар из четвертой урны.
Очевидно = 
, = 
.
2. Событие А уже произошло (вынули белый шар). Нужно найти так называемую переоцененную вероятность гипотезы В2 - 
. Применяем формулу Байеса
.
Замечание: при сравнении переоцененной вероятности с безусловной убеждаемся, что они различны.
Ответ:
1.Вероятность того, что из наугад взятой урны достали белый шар, равна 0,575.
2. Вероятность того, что белый шар оказался из четвертой урны, равна 0,348.
Распределение Пуассона
Задача №7
Корректура в 400 страниц содержит 800 опечаток. Найти вероятность того, что наугад взятая страница содержит 3 опечатки.
Решение.
Находим среднее число опечаток на одной странице 
Применяем формулу Пуассона 
для 
=3. Получаем, что искомая вероятность равна 
.
Локальная, интегральная теоремы Лапласа, теорема Бернулли.
Задача №8
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
По условию, n=243; k=70; p=0,25; q=0,75. Так как n=243 – достаточно большое число, воспользуемся локальной теоремой Лапласа:
, где 
.
Найдем значение x:
По таблице значений функции
найдем 
.
Искомая вероятность
Ответ:вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, равна 0,0231.
Задача №9
Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна p=0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.
Решение.
Воспользуемся интегральной теоремой Лапласа:
где Ф(x) – функция Лапласа,
а) по условию, n=100; p=0,8; q=0,2; k1=75; k2=90. Вычислим x¢ и x¢¢:
;
.
Учитывая, что функция Лапласа нечетна, т.е. Ф(-x)=-Ф(x), получим
.
По таблице значений функции 
найдем:
Ф(2,5)=0,4938; Ф(1,25)=0,3944.
Искомая вероятность
Р100(75;90)=0,4938+0,3944=0,8882.
б) требование, чтобы событие появилось не менее 75 раз, означает, что число появлений события может быть равно 75 либо 76, …, либо 100. Таким образом, в рассматриваемом случае следует принять k1=75, k2=100. Тогда
;
По таблице приложения 2 найдем Ф(1,25)=0,3944; Ф(5)=0,5.
Искомая вероятность
Р100(75;100)=Ф(5)-Ф(-1,25)=Ф(5)+Ф(1,25)=0,5+0,3944=0,8944.
в) События – “А появилось не менее 75 раз” и “А появилось не более 74 раз” противовоположны, поэтому сумма вероятностей этих событий равна единице.
Следовательно, искомая вероятность Р100(0;74)=1- Р100(75;100)=1-0,8944=0,1056.
Задача №10
Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,04.
Решение.
По условию, n=625; p=0,8; q=0,2; 
=0,04.
Требуется найти вероятность 
Воспользуемся формулой 
.
Имеем
.
По таблице приложения 2 найдем Ф(2,5)=0,4938. Следовательно, 2Ф(2,5)=2·0,4938=0,9876.
Ответ:искомая вероятность приближенно равна 0,9876.
Некоторые дополнительные задачи
Задача «О шарах»
В урне 2 белых, 3 черных, 1 красный шар. Наудачу извлекают 2 шара. Найти вероятность того, что это будут белый и черный шары.
Решение.
I способ (шары извлекаются последовательно).
Рассмотрим интересующее нас событие А - появление одного черного и одного белого шара – как сумму событий А1 – первый шар белый, второй черный и А2 – первый черный, второй белый.
Тогда А= А1 + А2, т.е. событие А состоит в появлении либо события А1, либо события А2.
В свою очередь, А1 есть произведение (совместное наступление) событий В1 и С1:
В1 – первым извлекли белый шар,
С1 – вторым извлекли черный шар.
Поскольку В1 и С1 события зависимые, то P(A1)=P(B1) ∙ 
(C1).
Найдем вероятность события B1.
Всего шаров в урне шесть, из них 2 белых. Следовательно, вероятность извлечь белый шар равна 2/6.
Найдем (С1). Событие С1 наступает после события В1, в урне осталось 5 шаров, из них 3 черных.
Следовательно, (С1)= 
.
Тогда P(A1)=P(B1) ∙ (C1)= 
.
Аналогично найдем вероятность события А2 (сначала черный, потом белый).
Введем события В2 и С2:
В2 ‑ первым появился черный шар,
С2 – вторым появился белый шар.
Тогда P(B2) = 
и искомая вероятность P(A2)=P(B2) ∙ 
(C2)= 
.
Наконец, интересующая нас вероятность события А равна
P(A)=P(A1) + P(A2) = 
.
II способ (шары извлекаются одновременно)
Согласно классической формуле вероятности P=m/n, где m - число благоприятных исходов, n – общее число исходов.
Общее число n исходов опыта в данной задаче (извлечение двух шаров из шести возможных) определяется числом способов, какими можно извлечь два шара из шести. Это число сочетаний из шести по два, n= 
.
При этом благоприятное число исходов m = 
- из двух белых извлекаем один { 
} способами и из трех черных извлекаем один { 
} способами.
Применяя формулу сочетаний 
, получим
. Окончательно, P= 
.
Ответ: вероятность того, что из двух извлеченных наудачу шаров будет один белый и один черный, равна .
Задача «О лгунах»
В городе N жителей. Некто пустил слух, рассказав «новость» 1-му жителю. Тот рассказал следующему и т.д. Какова вероятность того, что 10-й житель расскажет «новость» тому, кто узнал ее первым.
Решение.
Для того, чтобы произошло интересующее нас событие А – 10-й житель рассказал «новость» первому, необходимо, чтобы первые девять этого не сделали. Очевидно, что первые два жителя из этих девяти не сделают этого с вероятностью, равной единице.
Остальные семь – с вероятностью, равной 
. Десятый же расскажет «новость» первому с вероятностью 
, т.к. благоприятный исход один, общее - N-2, поскольку в общем случае новость рассказывается любому жителю из N за исключением того, от кого услышана.
Таким образом, искомая вероятность определяется как 
.
ТИПОВЫЕ РАСЧЕТЫ
I вариант
1. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры нечетные.
2. N охотников договорились стрелять по дичи в такой последовательности: следующий стреляет лишь в случае промаха предыдущего. Вероятность попадания каждого равна ½. Найти вероятность того, что будет произведено 2 выстрела.
3. Слово Т О Л О К Н О разрезали на буквы, перемешали их и извлекли 3 буквы. Найти вероятность того, что получилось слово Т О Н.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 200 монет.
5. Какова вероятность того, что при 10 бросках игральной кости три очка появятся ровно 1 раз?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,9, а завода №2 – 0,7. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 2. Применяя закон Пуассона, найти вероятность того, что за 2 минуты поступит 3 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 100 анализах будет получено ровно 75 положительных результатов.
9. В партии 60% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 200 деталей первосортных не менее 120 и не более 150 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,8.
II вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры.
Найти вероятность того, что в выборке все цифры одинаковые.
2. В ряду 10 стульев. Какова вероятность того, что при произвольном рассаживании десяти человек 3 определенных лица окажутся рядом?
3. Слово Б У Л А В К А разрезали на буквы, перемешали их и извлекли 4 буквы. Найти вероятность того, что получилось слово Л А В А.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,02.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 100 монет.
5. Какова вероятность того, что при 10 бросках игральной кости число очков, кратное трем, появится ровно три раза?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,8, а завода №2 – 0,6. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 3. Применяя закон Пуассона, найти вероятность того, что за 1 минуту поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,7. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 150 анализах будет получено ровно 100 положительных результатов.
9. В партии 50% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 300 деталей первосортных не менее 160 и не более 200 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,99, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,1.
Вероятность попадания при одном выстреле равна 0,9.
III вариант
1. На карточках написаны цифры от 1 до 9. Карточки перемешивают, наугад берут 4 из них и раскладывают в порядке появления. Какова вероятность получить при этом число 5678?
2. Двенадцать человек садятся за круглый стол. Какова вероятность того, что при этом два определенных лица сядут порознь?
3. Слово В О Д О Р О Д разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово Д В О Р.
4. Чему равна вероятность наступления события в каждом испытании, если произведено 49 независимых испытаний, а наивероятнейшее число наступлений события из них равно 30?
5. Какова вероятность того, что при 10 бросках игральной кости три очка появятся ровно три раза?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,7, а завода №2 – 0,5. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 4. Применяя закон Пуассона, найти вероятность того, что за 0,5 минуты поступит 3 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,75. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 20 анализах будет получено ровно 13 положительных результатов.
9. В партии 70% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 400 деталей первосортных не менее 260 и не более 300 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,85, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,8.
IV вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры.
Найти вероятность того, что в выборке три цифры одинаковые.
2. В ряду 9 стульев. Какова вероятность того, что при произвольном рассаживании 9 человек 3 определенных лица окажутся рядом?
3. Слово П О Л О Т Н О разрезали на буквы, перемешали их и извлекли 3 буквы. Найти вероятность того, что получилось слово Л О Т.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,02.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 200 монет.
5. Какова вероятность того, что при 10 бросках игральной кости число очков, кратное трем, появится ровно 4 раза?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,5, а завода №2 – 0,8. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 5. Применяя закон Пуассона, найти вероятность того, что за 0,2 минуты поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 30 анализах будет получено ровно 20 положительных результатов.
9. В партии 80% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 500 деталей первосортных не менее 350 и не более 450 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,9.
V вариант
1. Набирая номер телефона, абонент забыл последние две цифры, но помня, что эти цифры различны, набрал наугад. Определить вероятность того, что набраны нужные цифры.
2. Буквенный замок содержит на общей оси 4 диска, каждый из которых разделен на 6 секторов с различными нанесенными на них буквами. Замок открывается, когда каждый диск занимает определенное положение относительно корпуса замка.
Определить вероятность открытия замка, если установлена произвольная комбинация букв.
3. Слово С Е Р Е Б Р О разрезали на буквы, перемешали и извлекли 3 буквы. Найти вероятность того, что получилось слово Б О Р.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,03. Найти наивероятнейшее число случаев правильной работы автомата, если опущено 150 монет.
5. Какова вероятность того, что при 10 бросках игральной кости три очка не выпадут ни разу?
6. Сборщик получил 2 коробки одинаковых деталей с завода №1 и 3 коробки деталей с завода №2. Вероятность того, что деталь завода №1 стандартна, равна 0,6, а завода №2 – 0,8. Из наудачу взятой коробки сборщик наудачу извлек деталь.
А. Найти вероятность того, что извлечена стандартная деталь.
В. Извлеченная деталь оказалась стандартной. Найти вероятность того, что она 1) с завода №1; 2) с завода №2.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 1. Применяя закон Пуассона, найти вероятность того, что за 3 минуты поступит 4 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,85. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 25 анализах будет получено ровно 22 положительных результатов.
9. В партии 90% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 600 деталей первосортных не менее 520 и не более 560 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,95, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,8.
VI вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры. Найти вероятность того, что в выборке только 2 одинаковые цифры.
2. В ряду 8 стульев. Какова вероятность того, что при произвольном рассаживании 8 человек 3 определенных лица окажутся рядом?
3. Слово С У Л Т А Н разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово С Т А Н.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 250 монет.
5. Производится 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,8. Найти вероятность ровно 5-ти попаданий.
6. Имеются три урны с шарами. В первой 4 белых и 3 черных, во второй 5 белых и 2 черных, в третьей 2 белых и 5 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 2. Применяя закон Пуассона, найти вероятность того, что за 2 минуты поступит 5 вызовов.
8. Вероятность положительного результата при химическом анализе равна 0,9. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 35 анализах будет получено ровно 30 положительных результатов.
9. В партии 40% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 100 деталей первосортных не менее 40 и не более 50 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,7.
VII вариант
1. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нем все цифры нечетные.
2. Из 11 билетов выигрышными являются 3. Определить вероятность того, что среди взятых наудачу четырех билетов два выигрышных.
3. Слово В Ы Б О Р К А разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово К Р А Б.
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,03.
Найти наивероятнейшее число случаев правильной работы автомата, если опущено 50 монет.
5. Производится 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,8. Найти вероятность ровно 4-х попаданий.
6. Имеются три урны с шарами. В первой 3 белых и 7 черных, во второй 4 белых и 6 черных, в третьей 5 белых и 5 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 3. Применяя закон Пуассона, найти вероятность того, что за 1 минуту поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,6. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 100 анализах будет получено ровно 55 положительных результатов.
9. В партии 30% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 200 деталей первосортных не менее 60 и не более 70 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,95, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,75.
VIII вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры. Найти вероятность того, что в выборке по 2 пары одинаковых цифр.
2. Семь человек случайным образом садятся на семь поставленных в ряд стульев. Какова вероятность того, что 3 определенных лица окажутся рядом?
3. Слово К Р Е П О С Т Ь разрезали на буквы, перемешали и извлекли 4 буквы. Найти вероятность того, что получилось слово П О С Т.
4. Сколько нужно взять деталей, чтобы наивероятнейшее число годных было равно 50, если вероятность наугад взятой детали оказаться бракованной равна 0,1?
5. Производится 10 выстрелов по мишени. Вероятность попадания при одном выстреле 0,9. Найти вероятность того, что будет не менее 5 попаданий.
6. Имеются три урны с шарами. В первой 4 белых и 5 черных, во второй 3 белых и 6 черных, в третьей 2 белых и 7 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 4. Применяя закон Пуассона, найти вероятность того, что за минуту поступит 2 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,65. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 40 анализах будет получено ровно 25 положительных результатов.
9. В партии 20% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 300 деталей первосортных не менее 50 и не более 60 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,9, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,05.
Вероятность попадания при одном выстреле равна 0,9.
IX вариант
1. На карточках написаны цифры от 1 до 9. Карточки перемешивают, наугад берут 4 из них и раскладывают в порядке появления. Какова вероятность получить нечетное число?
2. N охотников стреляют по дичи в такой последовательности: каждый стреляет лишь в случае промаха предыдущего. Вероятность попадания каждого – ½.
Найти вероятность того, что будет произведено N-2 выстрела.
3. Сколько перестановок можно получить из букв слова К О М И С С И Я?
Сколько перестановок начинается с первой буквы слова и кончается последней?
Сколько таких перестановок, в которых 2 одинаковые гласные стоят рядом?
4. Вероятность попадания в цель при одном выстреле – 0,8.
Найти наивероятнейшее число попаданий при 14 выстрелах.
5. Производится 10 выстрелов по мишеням. Вероятность попадания при одном выстреле 0,9.
Найти вероятность того, что будет не менее 9 попаданий.
6. Имеются три урны с шарами. В первой 4 белых и 4 черных, во второй 3 белых и 5 черных, в третьей 2 белых и 6 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны; 2) из второй урны; 3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 5. Применяя закон Пуассона, найти вероятность того, что за 0,2 минуты поступит 3 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,5. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 45 анализах будет получено ровно 20 положительных результатов.
9. В партии 10% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 400 деталей первосортных не менее 35 и не более 45 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,85, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,9.
X вариант
1. Из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 выбирают с возвратом 4 цифры.
Найти вероятность того, что в выборке все цифры разные.
2. Буквенный замок содержит на общей оси 3 диска, каждый из которых разделен на 8 секторов с различными нанесенными на них буквами. Замок открывается, когда каждый диск занимает определенное положение относительно корпуса замка. Определить вероятность открытия замка, если установлена произвольная комбинация букв.
3. Слово К В А Р Т И Р А разрезали на буквы, перемешали и извлекли 3 буквы. Найти вероятность того, что получилось слово Т И Р.
4. Вероятность изготовления стандартной детали в некоторых условиях – 0,98. Найти наивероятнейшее число стандартных деталей из 625.
5. Какова вероятность того, что при десяти бросаниях монеты «орел» выпадет ровно пять раз?
6. Имеются три урны с шарами. В первой 2 белых и 4 черных, во второй 3 белых и 3 черных, в третьей 1 белых и 5 черных. Выбирают наугад одну из урн и вынимают 1 шар.
А. Найти вероятность того, что он белый.
В. Вынутый шар оказался белым. Найти вероятности того, что он:
1) из первой урны;
2) из второй урны;
3) из третьей урны.
7. Среднее число вызовов, поступающих на АТС за 1 минуту, равно 6. Применяя закон Пуассона, найти вероятность того, что за 0,5 минуты поступит 4 вызова.
8. Вероятность положительного результата при химическом анализе равна 0,55. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 50 анализах будет получено ровно 25 положительных результатов.
9. В партии 75% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 500 деталей первосортных не менее 350 и не более 400 штук.
10. Применяя теорему Бернулли, определить, сколько нужно произвести выстрелов по мишени, чтобы с вероятностью, равной 0,99, относительная частота попаданий отличалась от постоянной вероятности по абсолютной величине не более чем на 0,1.
Вероятность попадания при одном выстреле равна 0,7.
XI вариант
1. Производится прием кодовых операций, содержащих 4 цифры от 1 до 4. Определить вероятность того, что в принятой комбинации цифры образуют последовательность 1, 2, 3, 4.
2. Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу пяти билетов один выигрышный.
3. Из букв слова М У Ж Е С Т В О составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность сработать автомату при опускании одной монеты неправильно – 0,01. Найти наивероятнейшее число случаев правильной работы автомата, если опущено 250 монет.
5. Вероятность попадания по быстродвижущейся цели при автоматической наводке орудия равна 0,7. Определить вероятность 5 попаданий при 10 выстрелах.
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,2; 0,5; 0,3. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,1; 0,2; 0,4.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов. Найти вероятность того, что 1) лампа принадлежит 1-й партии;
2) 2-й партии; 3) 3-й партии.
7. Корректура в 500 страниц содержит 1500 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,7. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 30 анализах будет получено ровно 25 положительных результатов.
9. В партии 70% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 1000 деталей первосортных не менее 500 и не более 700 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 40 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности, не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,7.
XII вариант
1. Производится прием кодовых операций, содержащих 4 цифры от 1 до 4. Определить вероятность того, что в принятой последовательности цифра 1 оказалась последней.
2. Из 15-ти билетов выигрышными являются 3. Определить вероятность того, что среди взятых наудачу четырех билетов один выигрышный.
3. Из букв слова М У З Ы К А Н Т составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. Вероятность попадания в цель при одном выстреле – 0,9.
Найти наивероятнейшее число попаданий при 15 выстрелах.
5. Вероятность того, что кинокамера, взятая напрокат, будет возвращена исправной, равна 0,8. Какова вероятность того, что из 4-х кинокамер, взятых напрокат, три окажутся неисправными?
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,4; 0,5; 0,1. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,7; 0,8; 0,9.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов.
Найти вероятность того, что 1) лампа принадлежит 1-й партии;
2) 2-й партии;
3) 3-й партии.
7. Корректура в 600 страниц содержит 1200 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 1 опечатку.
8. Вероятность положительного результата при химическом анализе равна 0,8. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 35 анализах будет получено ровно 24 положительных результатов.
9. В партии 80% деталей 1-го сорта. Применяя интегральную теорему Лапласа, найти вероятность того, что среди взятых наудачу 900 деталей первосортных не менее 700 и не более 800 штук.
10. Применяя теорему Бернулли, определить вероятность того, что при 30 выстрелах по мишени относительная частота попаданий отклонится от постоянной вероятности не более чем на 0,01.
Вероятность попадания при одном выстреле равна 0,7.
XIII вариант
1. Определить вероятность того, что номер первой встречающейся автомашины не содержит одинаковых цифр.
2. Из 15 билетов выигрышными являются 3. Определить вероятность того, что среди взятых наудачу шести билетов: а) оба выигрышных; б) оба проигрышных.
3. Из букв слова М У Ш К Е Т Е Р составляются четырехбуквенные слова.
Определить:
а) сколько таких слов можно получить?
б) сколько таких слов начинается с буквы «М»?
в) сколько таких слов заканчивается гласной буквой?
4. В результате многолетних наблюдений для некоторой местности было установлено, что вероятность первого июля быть дождливым днем равна 0,4. Найти наивероятнейшее число дождливых дней первого июля за ближайшие 50 лет.
5. Вероятность попадания в цель при одном выстреле – 0,85.
Найти вероятность 8 попаданий при 10 выстрелах.
6. Радиолампа, поставленная в телевизор, может принадлежать одной из трех партий с вероятностями 0,1; 0,2; 0,7. Вероятности того, что лампа проработает определенное число часов, равны соответственно 0,6; 0,7; 0,8.
А. Определить вероятность того, что наугад взятая лампа проработает заданное число часов.
В. Наугад взятая лампа проработала заданное число часов.
Найти вероятность того, что
1) лампа принадлежит 1-й партии;
2) 2-й партии; 3) 3-й партии.
7. Корректура в 700 страниц содержит 1400 опечаток. Применяя закон Пуассона, найти вероятность того, что наудачу взятая страница содержит 2 опечатки.
8. Вероятность положительного результата при химическом анализе равна 0,6. Применяя формулу Муавра-Лапласа, найти вероятность того, что при 40 анализах будет получено ровно 30 положительных результатов.
Читайте также:
lektsia.com
Теория вероятностей в азартных играх
- Основы теории вероятностей
Азартные игры привлекают людей уже очень давно, ведь выигрыш и проигрыш зависит от везения, случая и немного от умения игрока играть. Азартные игры бывают разнообразные – баккара, рулетка, очко, штос, лотерея, спортивные пари и все ставки в тотализаторе и другие, но всех их объединяет теория вероятности выигрыша и проигрыша.
Игра в рулетку
Основной элемент. Предвидеть случайность
Теории вероятности в истории
Теория вероятности в азартных играх проявила себя еще в XVII веке, благодаря Шевалье де Меру. Он придумал заключать пари с наибольшей вероятностью выигрыша, просчитав все варианты, он сначала выигрывал и из-за того, что с ним никто больше не хотел заключать пари, просчитал другой, как он думал выигрышный вариант. Он думал, что он будет выигрышным, как и первый, но немного просчитался. Чтобы понять, где он совершил ошибку, он обратился к математику Блезу Паскалю. Так, благодаря Шевалье и его теории вероятности в азартных играх, возникла новая наука. Многие ученые пытались просчитать разные возможности выигрыша и проигрыша в игре.
На грани безумия. Невероятная вероятность.
Что нужно брать во внимание, просчитывая варианты выигрыша?
Теория вероятности в азартных играх берет во внимание несколько категорий:
- Количество проводимых испытаний;
- Вероятность того, что событие случится в случае одного испытания;
- Степень уверенности в выигрыше;
- Случайность.
Если рассмотреть теорию вероятности в лотереи, то можно применить такую формулу:
n*(n-1)*(n-2)*…*(n-(m-1))/ m*(m-1)*(m-2)*…*1
n – общее количество шариков;m – количество, которое нужно угадать.
В лотереи из 49 шаров, где нужно угадать 6 шаров, расчет будет выглядеть так:
49 * 48 * 47 * 46 * 45 * 44 / 6 * 5 * 4 * 3 * 2 * 1 = 13 983 816
13 983 816 – число, степени уверенности в выигрыше.
Игральные кубики
Для разных азартных игр, теория вероятности будет разная. Бросая игральный кубик, у игрока вероятность выигрыша составляет 16,66%, то есть возможность, что выпадет необходимая комбинация — 1, делится на число возможных комбинаций — 6:
1 / 6 = 16,66 %.
Такое событие, как выигрыш может быть: случайным, невозможным или достоверным.
Достоверное событие – событие, которое произойдет в любом случае если соблюдать все условия, для его совершения. Играя в кости, рано или поздно выиграешь.
Случайное – случайный выигрыш, например, когда человек начал играть и сам того не ожидая, сразу же выиграл.
Невозможное событие – когда возможность выигрыша равна 0.
Закон больших чисел в теории вероятности
Яков Бернулли, исследуя теорию вероятности выигрыша, установил, что чем больше количество испытаний, количество одних или других событий будет стремиться к вероятности, умноженной на количество этих испытаний. Этот закон срабатывает, если в одну игру сыграть примерно 10000 раз. Этот закон он установил бросая монетку.
В случае с азартными играми этот закон действует также Игрок при огромном количестве игр выиграет столько же сколько и проиграет.
Если человек будет бросать кубик 6000 раз, а сумма ставки — 1 $, то он выиграет:
1 / 6 * 6000 * 5$ = 5000$ и проиграет также 5000$, ведь 5 / 6 * 6000 * 1 = 5000$.
Для того чтобы закон больших чисел начал работать – нужно верить в результат и проявлять усердие в игре. Все в мире выравнивается, в том числе и результат игры, но бывают случаи, когда закон не действует из-за везения или невезения человека.
Проблема количества испытаний или парадокс Салиу в теории азартной игры
Вероятность выигрыша в игре можно рассчитать, но расчеты – еще не гарантия того, что человек выиграет. Если рассмотреть игру в рулетку, то вероятность выигрыша 1 / 38, но сыграв 38 раз человек может и не выиграть вовсе. В этом случае человек задумывается о том, что удача отвернулась от него.
Вероятность выигрыша в азартной игре
В мире существует огромное количество азартных игр, и вероятность выигрыша у них совершенно разные. Все зависит от количества выигрышных комбинаций. Количества игроков, везения, суммы ставок.
Для того чтобы увеличить выигрыш можно играть по-разному. Одни играют много, но на маленькие суммы, другие играют мало, но по крупному. Считается, что увеличить количество денег проще, если играть мало, но делать большие ставки – тогда выигрыш максимальный. Если сыграть в рулетку выбрав цвет или четность, то вероятность выигрыша будет примерно 48 %. Играя с большими ставками вероятность, выиграть огромные деньги увеличивается. Вероятность выигрыша в некоторых играх зависит от везения, но в некоторых вероятность можно увеличить благодаря возможности выбора – карточные игры.
Играя в блекджек или покер, человек может выиграть или проиграть, сделав неправильный выбор. Выигрыш в таких играх зависит не только от теории вероятности, но и от мастерства игрока и его умения держать эмоции под контролем .
Играем в карты
Важность соблюдения стратегии азартной игры
Играя в азартные игры, люди, которые впервые столкнулись с игрой и теорией вероятности выигрыша, очень часто совершают одну и ту же ошибку – гонятся за выигрышем, каждый раз ставят на разные числа, цвета. В таком случае возможность выигрыша постоянно уменьшается. Если ставить на одно и то же, то теория вероятности сработает рано или поздно. Если игрок умеет играть, он соблюдая свою стратегию игры, может длительное время играть в минус, но в конечном результате выйти в плюс.
Азартные игры – это всегда интересно, но играя нужно постоянно трезво оценивать свои возможности на выигрыш или проигрыш. Удача – очень часто изменчива и если следовать за принципами теории вероятности, то выиграв несколько раз, потом можно все проиграть, если не остановиться. Бывали случаи, когда бедные люди выигрывали за несколько часов миллионы и проигрывали их в тот же день, оставаясь с тем, с чем пришли. А другие выигрывали и вовремя останавливались, что давало возможность полностью поменять свою жизнь к лучшему.
Теория вероятности в азартной игре может помочь выиграть, но если человек все хорошо продумает, просчитает и останется верным выбранной стратегии. В любом случае всегда есть возможность выигрыша и возможность проигрыша в азартной игре, но если накапливать знания и умения играть, то в некоторых случаях это дает возможность увеличить шансы на выигрыш.
Почему математики не тратят время на лотереи
www.13min.ru
